Це припущення не таке нешкідливе, як здається. Розглянемо рівняння
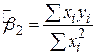 .
.
Якщо всі значення Х збігаються, то 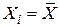 і знаменник дробу обертається в нуль, що робить неможливим знаходження параметрів регресії. У нашому випадку зрозуміло, що при малій мінливості Х не можна пояснити велику мінливість Y. Потрібно пам’ятати, що мінливість обох змінних Х і Y є основоположним моментом регресійного аналізу. Коротше кажучи, змінні повинні змінюватися.
і знаменник дробу обертається в нуль, що робить неможливим знаходження параметрів регресії. У нашому випадку зрозуміло, що при малій мінливості Х не можна пояснити велику мінливість Y. Потрібно пам’ятати, що мінливість обох змінних Х і Y є основоположним моментом регресійного аналізу. Коротше кажучи, змінні повинні змінюватися.
Припущення 9 - регресійна модель вибирається коректно
Інакше кажучи, відсутня помилка зсуву в моделі, що застосовується в емпіричному аналізі.
Ми вже зазначали, що класична регресійна модель передбачається вибраною коректно. Економічні дослідження починаються з вибору економетричної моделі, що лежить в основі предмета дослідження. При цьому повинні бути з’ясовані такі питання: 1) які змінні повинні бути включені в модель? 2) який вигляд функціональної залежності? 3) які припущення імовірності робляться відносно 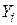 і
і 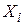 і
і 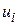 , що входять у модель?
, що входять у модель?
Ці питання важливі , оскільки, як ми побачимо, не включення суттєвих змінних у модель, або неправильний вибір функціональної залежності, або неправильні стохастичні припущення роблять дуже сумнівними отримані при економетричному аналізі результати.
Припустимо, що ми вибрали такі дві моделі для встановлення залежності рівнів інфляції і безробіття:
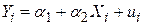 , ,
| (2.2.5) |
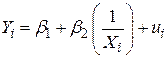 , ,
| (2.2.6) |
де 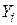 – рівень інфляції, а
– рівень інфляції, а 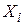 – рівень безробіття.
– рівень безробіття.
Модель (2.2.5) лінійна і за параметрами, і за змінними, а (2.2.6) нелінійна за параметром 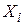 . На рис. 2.9 зображені ці моделі. Якщо модель (2.2.6) коректна, то модель (2.2.5) дає нам неправильний прогноз: між точками А і В, для будь-яких значень
. На рис. 2.9 зображені ці моделі. Якщо модель (2.2.6) коректна, то модель (2.2.5) дає нам неправильний прогноз: між точками А і В, для будь-яких значень 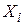 модель (2.2.5) дає завищені середні значення Y, тоді як зліва від А або справа від Y вона дає занижені середні значення Y.
модель (2.2.5) дає завищені середні значення Y, тоді як зліва від А або справа від Y вона дає занижені середні значення Y.
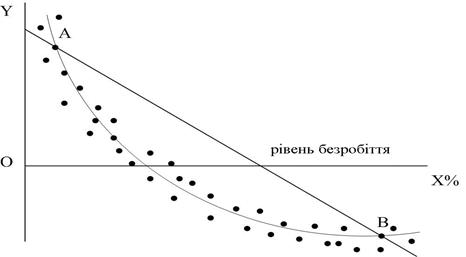
Рис. 2.9. Дві моделі залежності рівнів інфляції та безробіття
Припущення 10 - відсутність точної мультиколінеарності
Тобто між пояснювальними змінними відсутня точна мультиколінеарність.
Дата добавления: 2016-07-27; просмотров: 1900;











