АППРОКСИМАЦИЯ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ

Изучая способы интерполирования, мы получили различные виды интерполяционных многочленов, которые в точности совпадают со значениями данной функции в узлах интерполирования.

Однако точное воспроизведение значений функции в узловых точках далеко не всегда является необходимым, а иногда даже нецелесообразно.

Так например, если число точек (n+1) велико, то глобальный интерполяционный многочлен будет высокой степени (n). Работать с ним неудобно, да и при его вычислении будет накапливаться вычислительная погрешность (об этом уже говорилось ранее).

Кроме того, табличные данные чаще всего являются результатами каких-то измерений и содержат ошибки – как случайные, так и систематические (по нашей классификации – неустранимые). Построение аппроксимирующего многочлена с условием обязательного прохождения его графика через эти экспериментальные точки означало бы тщательное повторение допущенных при измерениях ошибок.

Выход из этого положения может быть найден выбором такого многочлена (степени более низкой, чем n!), который хотя и не дает точных значений функции в узлах, но достаточно близко к ним подходит.

Словам «близко подходит» можно придавать различный смысл, и в зависимости от этого получаются различные задачи аппроксимации, решениями которых являются различные аппроксимационные многочлены. Иными словами, возможны различные критерии аппроксимации.

Примечание 1. О равномерной аппроксимации.

При равномерной аппроксимации требуют, чтобы максимум модуля разности между значениями данной функции y=f(x) и аппроксимирующей функции y=F(x) не превосходил некоторой величины, которую можно считать за меру приближения, то есть

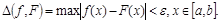
В этом случае говорят, что функция F(x) равномерно аппроксимирует функцию f(x) с точностью e на отрезке [a, b].

Если в качестве аппроксимирующей функции выбран многочлен P(x)с такими коэффициентами, что величина D минимальна на данном отрезке, то говорят о многочлене наилучшего равномерного приближения. Теорема Вейерштрасса говорит о его существовании и единственности[10].

Не будем подробно останавливаться на равномерном приближении, отметим только, что многочлен

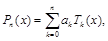
составленный по полиномам Чебышева, является минимизирующим многочленом.

Конец примечания 1.

На практике часто допускают, что отдельные отклонения

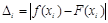
могут быть и велики, но требуют, чтобы отклонения F(x) от f(x) были малы в среднем. Наиболее удобная форма требования «близости в среднем» состоит в том, чтобы сумма квадратов отклонений F(x) от f(x) в узлах аппроксимации не превосходила некоторой заданной величины.

Таким образом, мерой отклонения здесь является величина

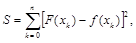
называемая квадратичным отклонением.

Метод наименьших квадратов заключается в отыскании такой аппроксимирующей функции F(x), которая дает наилучшее приближение в среднем, то есть обеспечивает минимум квадратичного отклонения.

В общем случае в качестве аппроксимирующей функции может выступать любая функция F(x, c₀, c₁, ... ,c_m) c неизвестными параметрами c₀, c₁, ..., c_m, которые могут входить линейным или нелинейным образом в выражение для F.

Часто в качестве аппроксимирующих функций выбирают обобщенные полиномы:

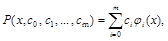
где {j_i(x)} – заданная система функций (в частности, полиномов, например, j_i(x)ºxⁱ ).