Метод наименьших квадратов в нелинейном случае
Как быть в том случае, когда поведение экспериментальных точек, для которых мы хотим построить аппроксимирующую функцию, не похоже на поведение многочленов 1-ой, 2-ой и т.д. степени? Или, более того, тот физический процесс, который мы изучаем в эксперименте, по теоретическим соображениям должен описываться некоторой функцией F(x, c0, c1, ... ,cm) с коэффициентами, нелинейным образом входящими в функциональную зависимость?
Если применять метод наименьших квадратов в традиционном виде, то получающаяся система уравнений для нахождения сi будет нелинейная:
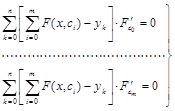 .
.
Способы решения систем нелинейных уравнений известны (см. главу 5), но это сложные и трудоемкие способы. Но можно облегчить себе задачу: с помощью подходящей замены переменных постараться линеаризовать задачу, а затем уже в линеаризованной задаче для аппроксимации использовать многочлен (аналогичная идея применялась в нелинейной интерполяции).
Примечание 3. Обработка экспериментальных данных: подбор эмпирических формул.
Процесс подбора аппроксимирующей формулы для найденной из опыта функциональной зависимости y=f(x) состоит из двух этапов. Сначала выбирается вид формулы (причем стараются не перегружать ее коэффициентами: чем проще формула, тем она понятнее, тем яснее физический смысл входящих в нее параметров). Затем с помощью метода наименьших квадратов определяются численные значения параметров, для которых приближение к данной функции оказывается наилучшим.
В таблице 2.1 приведены некоторые простейшие эмпирические формулы, допускающие линеаризацию, то есть приведение к виду
h=a×x+b,
где h=j(х,у), x=f(х,у), а a и b – числовые коэффициенты.
Таблица 2.1 – Формулы линеаризации
| Эмпирическая формула | 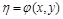
| 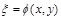
| 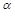
| 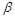
|
| y=axb | h=lg(y) | x=lg(x) | b | lg(a) |
| y=a×bx | h= lg(y) | x=x | lg(b) | lg(a) |
| y=a+b/x | h=y | x=1/x | b | a |
| y=1/(ax+b) | h=1/y | x=x | a | b |
| y=x/(ax+b) | h=x/y | x=x | a | b |
| y=a×lg(x)+b | h=y | x=lg(x) | a | b |
Конец примечания 3.
Приведем несколько примеров, иллюстрирующих метод наименьших квадратов.
Пример 1. Пусть табличная зависимость y=f(x) напоминает график квадратного трехчлена, то есть в качестве аппроксимирующей функции можно выбрать P(x,a,b,c)=ax2+bx+c. Тогда квадратичное отклонение имеет вид
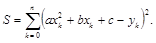
Система уравнений для определения коэффициентов a,b,c:
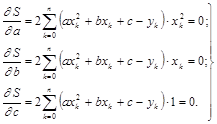
После преобразований
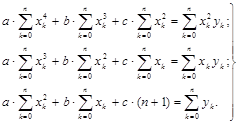
Все суммы – числовые константы, определяемые по табличным значениям.
Полученная система линейных алгебраических уравнений решается методами, которые будут рассмотрены в главе 4.
Пример 2. Аппроксимировать функцию у=х1/2 на отрезке xÎ[0;4] обобщенным полиномом второй степени, построенном на полиномах Лежандра.
Сделаем замену переменных t=x/2–1 и перейдем к отрезку tÎ[–1;1].
Аппроксимируемая функция примет вид 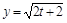 . Аппроксимирующая – F(t)=c0P0(t)+ c1P1(t)+ c2P2(t), где Pi(t) – полиномы Лежандра:
. Аппроксимирующая – F(t)=c0P0(t)+ c1P1(t)+ c2P2(t), где Pi(t) – полиномы Лежандра:
P0(t)=1; P1(t)=t; P2(t)=(3t2–1)/2.
Тогда
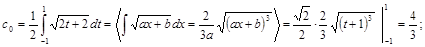
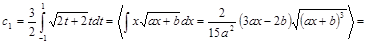
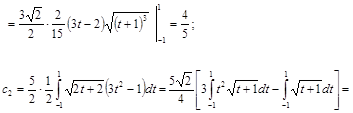
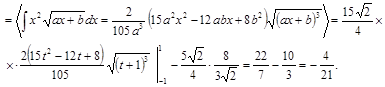
Таким образом, аппроксимирующая функция имеет вид
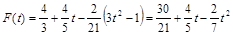
или
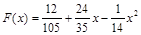 .
.
Пример 3.Методом наименьших квадратов провести аппроксимацию табличной функции
| x | |||||
| y | 0,20 | 0,28 | 0,33 | 0,37 | 0,39 |
В качестве аппроксимирующей функции взять F(x)=x/(ax+b).
Сделаем замену переменных h=x/y; x=х и пересчитаем таблицу в новых переменных:
| x | |||||
| h | 5,0 | 7,14 | 9,09 | 10,81 | 12,82 |
Аппроксимирующая функция примет вид F(x)=ax+b.
Тогда квадратичное отклонение
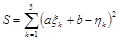 .
.
Минимизируя его, получаем систему линейных уравнений
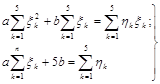
откуда
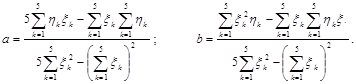
Вычисляя суммы по табличным значениям {xk ,hk}, находим а=1,93; b=3,18.
Таким образом, аппроксимирующая функция имеет вид:
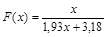 .
.
[1] approximo (лат.) - приближаюсь
[2] Доказывается, что в общем случае не существует способа вычисления алгебраического многочлена n-ой степени менее, чем за 2n арифметических действий.
[3] Полиномы Чебышева имеют еще одно замечательное свойство - ортогональность, но о нем поговорим позже.
[4] inter (лат.) – между; pole (лат.) – узел
[5] Пусть f(x)-непрерывная и дифференцируемая на [a,b] функция. Если f(a)=f(b), то найдется по крайней мере одна точка x0Î [a,b], в которой f¢(x0)=0. Следствие: между двумя нулями многочлена находится по крайней мере один нуль производной этого многочлена.
[6] Для нахождения трех коэффициентов полинома P1(x,y) необходимо решить три уравнения: 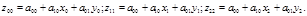 Главный определитель
Главный определитель 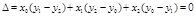 , если узлы лежат на одной прямой.
, если узлы лежат на одной прямой.
[7] spline (англ.) гибкая линейка. Будучи деформирована и проходя через фиксированные точки, линейка приобретает форму, при которой запасенная в ней упругая энергия минимальна. Это механическая интерпретация сплайн-интерполяции.
[8] Сплайн построенный таким образом обычно называют естественным кубическим сплайном.
[9] Это следует из (2.11) и (2.12).
[10] Каждую непрерывную функцию можно приблизить в метрике С как угодно хорошо алгебраическим многочленом достаточно высокой степени.
[11] Линейная зависимость: a0j0+a1j1+a2j2+...+amjm=0, где a0,...,am - не равные одновременно нулю числа.
Дата добавления: 2020-10-25; просмотров: 778;











