Аппроксимация ВАХ нелинейных элементов

Вольтамперные характеристики нелинейных элементов на практике чаще всего получают экспериментальным путем и представляют их или в графиче­ской форме [в виде графической диаграммы функции ], или в таблич­ной форме [в виде таблицы координат точек функции ]. При аналити­ческих методах расчета нелинейных цепей к ВАХ предъявляются требования, чтобы они были представлены в аналитической форме, т.е. в виде аналитиче­ского выражения.

Под аппроксимацией ВАХ понимают замену ее графической или таблич­ной формы на аналитическую. К уравнению аппроксимации предъявляются два противоречивых требования. Во-первых, уравнение аппроксимации должно по возможности точно описывать заданную ВАХ. Для более полного выполнения этого требования необходимо усложнять структуру этого уравнения. Во-вто­рых, уравнение аппроксимации, будучи введенным в систему уравнений Кирх­гофа, должно позволять решение этой системы доступными методами. Для вы­полнения этого требования структура этого уравнения должна быть по возмож­ности более простой. Таким образом, при выборе уравнения аппроксимации всегда приходится принимать компромиссное решение между этими двумя тре­бованиями.

Различают два способа аппроксимации нелинейных ВАХ – полная и ку­сочная (по частям).

В простейших случаях при монотонном характере изменения функции I(U) ВАХ может быть аппроксимирована полностью одним нелинейным урав­нением (рис. 212а).

В более сложных случаях, когда функция I(U) имеет несколько максиму­мов и минимумов, полная аппроксимация ВАХ одним уравнением становится проблематичной и нерациональной. В таких случаях применяют кусочную ап­проксимацию. Суть ее состоит в том, что вся ВАХ разбивается по тому или дру­гому принципу на отдельные участки (куски) (рис. 212б). Отдельные участки ап­проксимируются однотипными, но простыми по структуре, уравнениями, коэф­фициенты в которых изменяются при переходе от одного участка к другому. Если отдельные участки ВАХ аппроксимируются отрезками прямой 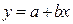, то такая аппроксимация получила название кусочно-линейной. Если отдельные участки ВАХ аппроксимируются квадратичной ( ) или кубической ( 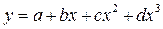) параболой, то отдельные участки получили название сплайнов, а сама аппроксимация – аппроксимации сплайнами. Кусочная ап­проксимация позволяет получить высокую степень приближения к заданной ВАХ, однако требует большого числа однотипных расчетов при определении коэффициентов в уравнениях аппроксимации.

Кусочная аппроксимация широко применяется при расчете нелинейных цепей на ЭВМ.