ИНТЕРПОЛИРОВАНИЕ СПЛАЙНАМИ
Интерполяция на больших отрезках нередко приводит к плохому приближению. С одной стороны, если взять мало узловых точек, то точность будет очень мала, с другой стороны, если взять много точек и использовать интерполяционный полином высокого порядка, то для него, несмотря на малую погрешность интерполяции, возрастает вычислительная погрешность, ухудшая общую точность решения.
Отчасти при решении таких задач оказывает помощь кусочная интерполяция более низкого порядка: интерполяция осуществляется по небольшому количеству узловых точек отрезка, а затем эти полиномы объединяются в единую интерполяционную формулу. Но при этом в точках стыковки обычно терпит разрыв уже первая производная, так что мы лишены возможности проводить дифференцирование получаемой интерполяционной функции.
Для того чтобы построить интерполяционную функцию с гладкими производными, можно использовать так называемую сплайн-интерполяцию.
Сплайн–функцией, или сплайном[7], называют кусочно-полиномиальную функцию, определенную на отрезке [a,b] и имеющую на этом отрезке некоторое число непрерывных производных. Разница между степенью сплайна и порядком наивысшей непрерывной на [a,b] производной называется дефектом сплайна.
В вычислительных методах большое распространение получили кубические сплайны.
Пусть на [a,b] задана непрерывная функция f(x). Bведем сетку а=х0<x1<¼<xn–1<xn=b и обозначим yk=f(xk), k=0,1,2,¼,n.
Интерполяционным кубическим сплайном называется функция S(x), удовлетворяющая следующим условиям:
а) на каждом отрезке [xk–1, xk], k=1,2,¼,n, функция S(x) является полиномом 3-ей степени (рис.2.5);
б) функция S(x), а также ее первая и вторая производные непрерывны на [a,b];
в) S(xk)=f(xk), k=0,1,...,n (условие интерполяции).
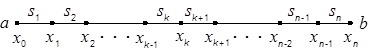
Рис.2.5 – Сетка и сплайны.
Будем искать кубический сплайн в виде
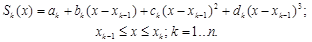
Следовательно, задача заключается в определении 4n коэффициентов ak, bk, ck, dk .
Используя свойства кубического сплайна, запишем систему уравнений для определения этих коэффициентов.
Из условия интерполяции имеем первую группу из 2n уравнений:
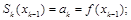 (2.8)
(2.8)
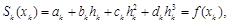 (2.9)
(2.9)
где 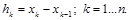
Теперь воспользуемся условиями непрерывности производных в узловых точках:
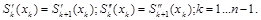
Так как
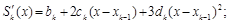
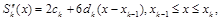
то эти условия составят вторую группу из 2n–2-х уравнений:
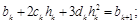 (2.10)
(2.10)
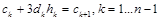 . (2.11)
. (2.11)
Недостает еще двух уравнений. Их получают из условий на границах отрезка.
Существует несколько способов задания граничных условий.
1. Заданы первые производные (“известен угол входа и выхода”):
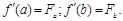
2. Заданы вторые производные (“гладкие условия”):
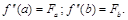
3. Равенство первых и вторых производных справа и слева (“периодические условия”):
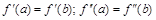 .
.
4. Непрерывность третьих производных в точках х1 и хn–1, то есть сплайн выражается одним кубическим многочленом на отрезках [x0, x2] и [xn–2, xn]:
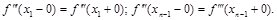
5. Возможны и комбинации этих условий: на одной границе задано условие одного типа, на другой – другого типа. Конкретный выбор условий зависит от конкретных требований задачи.
Пусть первые производные имеют постоянное значение[8].
Тогда
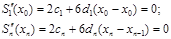
и получаем недостающие два уравнения
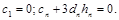 (2.12)
(2.12)
Для решения системы (2.8 – 2.12) можно предложить следующий способ.
Исключим ak из уравнений (2.8) и (2.9):
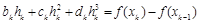
и подставим сюда dk из уравнений (2.11). Выражая bk , получаем
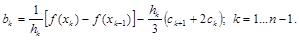
Сдвинув на единицу индекс у переменных, получаем выражение для bk+1:
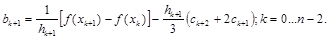
Теперь подставим bk , bk+1 , dk в уравнения (2.10) и получим систему уравнений для нахождения коэффициентов ck , k=1... n – 1.
Эта система представляет собой систему (n–1) линейных алгебраических уравнений с трехдиагональной матрицей.
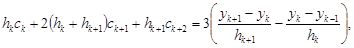
где с1=0 и cn+1=0[9].
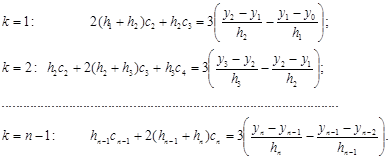
Ниже (глава 4) мы рассмотрим метод прогонки решения таких систем.
Дата добавления: 2020-10-25; просмотров: 790;











