Алгоритм моделирования системы электропривода по методу уравнений состояния

Уравнения (18) и (19) можно реализовать в нестандартном варианте составления программ по методу уравнений состояния, в которых отсутствует обращение к рабочей подпрограмме. Рис. 5 представлена блок-схема алгоритма моделирования СЭП по методу уравнений состояния.

Рис. 5. Блок-схема алгоритма моделирования по методу уравнений состояния

В алгоритме на рис. 5 реализуется интегрирование дифференциальных уравнений по методу Эйлера.

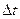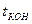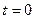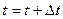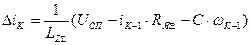Во втором блоке алгоритма производится ввод временных параметров моделирования: шага интегрирования и конечного времени моделирования . В третьем блоке устанавливается момент начала моделирования . В четвертом блоке начинается выполнение шага интегрирования ( ). В пятом блоке в соответствии с уравнением (16) определяется приращение тока на « » шаге интегрирования . В блоке 6 производится расчет тока на « » шаге интегрирования по уравнению 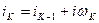. В седьмом блоке в соответствии с уравнением (17) определяется приращение скорости на « » шаге интегрирования 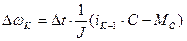. В блоке 8 производится расчет скорости на « » шаге интегрирования по уравнению 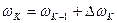. Во девятом блоке алгоритма производится вывод результатов моделирования. Во десятом блоке алгоритма осуществляется проверка текущего времени моделирования 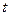с конечным временем моделирования 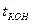. Если 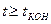, то процесс моделирования завершается, а иначе процесс продолжается, начиная с 4 блока алгоритма.

При решении других задач по моделированию СЭП необходимо изменить уравнения в блоках 5-8.