ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
| yo | y1 | y2 | ... | |
| x0 | z00 | z01 | z02 | ... |
| x1 | z10 | z11 | z12 | ... |
| x2 | z20 | z21 | z22 | ... |
| ... | ... | ... | ... | ... |
До сих пор мы рассматривали интерполирование функций одной независимой переменной y=f(x). На практике возникает также необходимость построения интерполяционных формул для функций нескольких переменных. Рассмотрим для простоты функцию двух переменных z=f(x,y), заданную таблично:
Обозначим zij=f(xi,yj), h1=xi+1–xi, h2=yj+1–yj (то есть узлы – равноотстоящие). Запишем общую формулу интерполяционного многочлена от двух переменных. Очевидно, она должна иметь следующий вид:
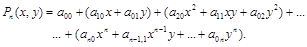
Например, интерполяционный многочлен Ньютона 2-ой степени для двух переменных выглядит следующим образом:
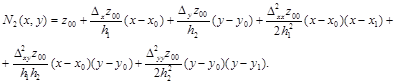 Здесь по аналогии с конечными разностями введены частные конечные разности первого порядка:
Здесь по аналогии с конечными разностями введены частные конечные разности первого порядка:
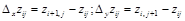
и второго порядка
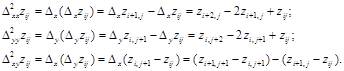
Какие существуют сложности при многомерном интерполировании?
1. Возрастает объем необходимой информации, то есть объем таблиц. Поэтому шаги по аргументам приходится брать довольно большими, что предъявляет жесткие требования к способу интерполирования.
2. Если для функции одной переменной степень полинома была взаимно однозначно связана с числом узлов, то для двух переменных полином n-ой степени Pn(x,y) имеет (n+1)(n+2)/2 узлов. Если число узлов не соответствует этой формуле, то часть коэффициентов при высших степенях приходится задавать произвольно (например, нули), что, естественно, влияет на точность аппроксимации.
3. Не всякое расположение узлов допустимо. В одномерном случае узлы не должны совпадать. Теперь же, например, при линейной интерполяции полиномом P1(x,y) необходимо, чтобы узлы не лежали на одной прямой в плоскости (x,y)[6]. При интерполяции квадратичным полиномом P2(x,y) требуется, чтобы узлы не лежали на кривой второго порядка. Такие условия проверять в общем случае довольно сложно, поэтому для хорошей интерполяции строят регулярную сетку. Наиболее удобная – прямоугольная сетка (рис.2.4).
Пусть, например, задана таблица zi,j=f(xi,yj ) и требуется найти f(x,y). Сначала проводим одномерную интерполяцию (лагранжеву или ньютонову) по строкам, то есть для каждого фиксированного j находим L(x,y0), L(x,y1 ),..., L(x,ym ).
Затем проводим одномерную интерполяцию по столбцам, то есть по значениям L(x,yj ) находим L(x,y).
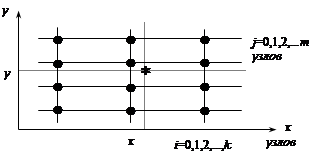 |
| Рис.2.4 – Интерполирование функции двух переменных. |
Дата добавления: 2020-10-25; просмотров: 1073;











