Аппроксимация модели объекта в виде n последовательных звеньев

Полученная в результате процедуры идентификации в пакете MatLab передаточная функция статической непрерывной модели исследуемого ТОУ представляет собой неоднородное линейное дифференциальное уравнение четвертого порядка:

,

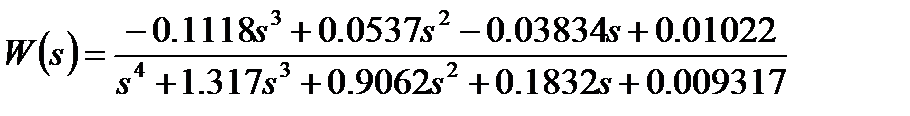которое не соответствует ни одному из существующих типовых динамических звеньев и не позволяет выполнить синтез регулятора или корректирующего звена для обеспечения заданных значений параметров качества регулирования. Таким образом, необходимо выполнить аппроксимацию модели объекта, представив ее в виде соединения типовых динамических звеньев.

Экспериментальные переходные характеристики (кривые разгона) устойчивых объектов второго и более высоких порядков с запаздываем (или без) имеют характерный S-образный вид (рис. 23).

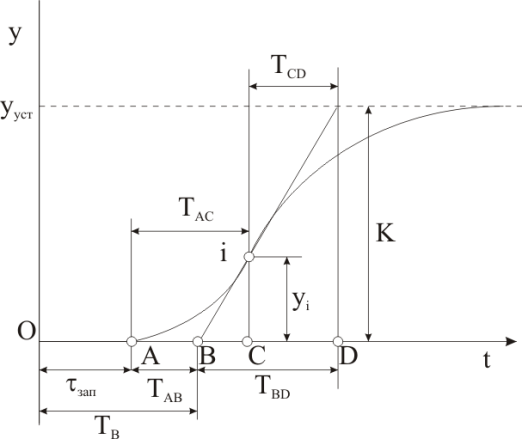
Рисунок 23 – Определение параметров модели объекта по экспериментальной характеристике

По графику экспериментальной характеристики переходного процесса (кривой разгона) определяем установившиеся значение выходной величины и коэффициент усиления соответственно:

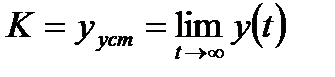, (11)

Характерной точкой на кривой разгона динамического звена является точка перегиба i, геометрический смысл которой заключается в том, что график переходной характеристики переходит в ней с одной стороны касательной на другую.

Через точку перегиба i проводим касательную до пересечения с осью Ot (точка В на рис. 23) и прямой 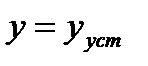. Соотношение длин отрезков CD и BD позволит установить порядок исследуемого динамического звена:

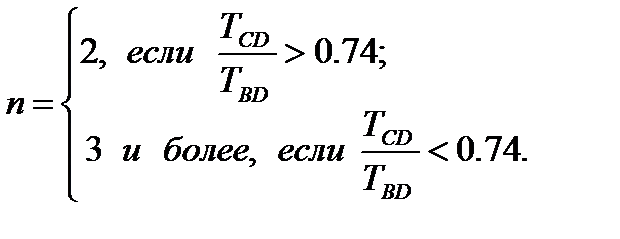
На следующем этапе определяется коэффициент демпфирования 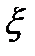по номограмме, представленной на рис. 24, для рассчитанного на предыдущем шаге соотношения 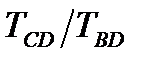и постоянная времени Т типового колебательного звена из соотношения:

.

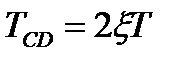Принятое значение коэффициента демпфирования позволит уточнить положение точки А на графике переходной характеристики (рис. 22) по соотношению 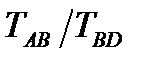на номограмме (рис. 24) и вычислить время транспортного запаздывания:

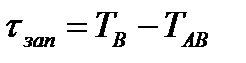. (12)

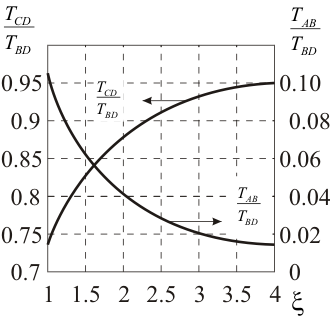
Рисунок 24 – Номограмма для определения параметров модели объекта

В случае, если соотношение 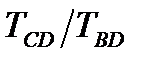меньше 0,74, то в общем виде передаточную функцию технологического объекта управления запишем следующим образом:

.

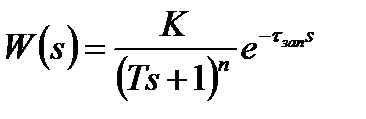Коэффициент усиления рассчитывается аналогично, как было сделано выше, по формуле (11). Число n статических звеньев первого порядка с одинаковыми значениями постоянных времени определим с помощью номограммы, показанной на рис. 25.

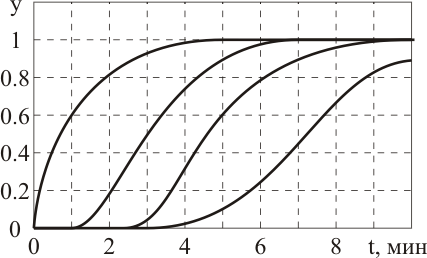
Рисунок 25 – Переходные характеристики устойчивых объектов разного порядка

На графике (рис. 26) проводим касательную через точку перегиба i и определяем отношение 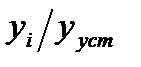(как это проделано на рис. 23), значение округляем до ближайшего меньшего табличного значения (табл. 3) и принимаем за n.

Таблица 3 – Данные для определения параметров передаточной функции системы по переходной характеристике

n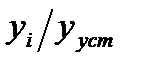
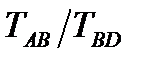
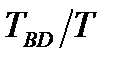
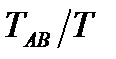
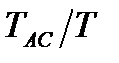
	0.264	0.104	2.718	0.282
	0.323	0.218	3.695	0.805
	0.353	0.319	4.463	1.425
	0.371	0.410	5.119	2.100

Затем по графику (рис. 26) определяют длину отрезка BD – 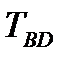и, используя для найденного порядка n табличное значение 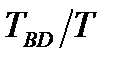(табл. 3), рассчитывают постоянную времени Т. Далее из таблицы 3 с учетом вычисленных значений параметров: 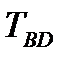и n, находим 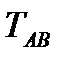и время транспортного запаздывания по формуле (12).

Для рассматриваемого технологического объекта управления характерно как транспортное, так и переходное запаздывание. Первое обусловлено транспортировкой вещества (воздуха) через трубопроводы, а второе – высоким порядком исследуемого ТОУ и близкими значениями постоянных времени типовых динамических элементов, из которых он составлен. Наличие запаздывания в САУ осложняет задачу регулирования технологического параметра на объекте, поэтому ее стремятся уменьшить: устанавливают чувствительный элемент первичного измерительного преобразователя и исполнительное устройство как можно ближе к объекту управления.

Выполним идентификацию модели ТОУ по выше описанной методике по переходной характеристике объекта (рис.26). Вычислим значения характерных временных интервалов и выходного сигнала в точке перегиба:

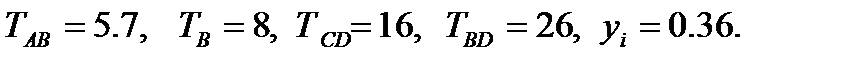
Поскольку соотношение ( 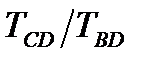) равно 0,61, порядок исследуемого технологического объекта будет выше второго. Для уточнения значения рассчитаем соотношение ( 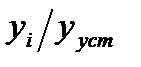)= 0,327. Из таблицы 3, округлив до ближайшего меньшего, получим .

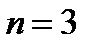Наличие на графике переходного процесса (рис. 26) участка, на котором при изменении входного сигнала выходной остается неизменным, свидетельствует о наличии запаздывания. Таким образом, ТОУ можно представить в виде последовательного соединения трех апериодических звеньев первого порядка и типового звена запаздывания, передаточная функция ресивера в результате опишется выражением вида:

.

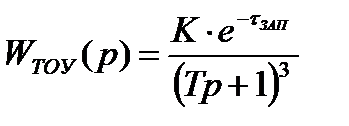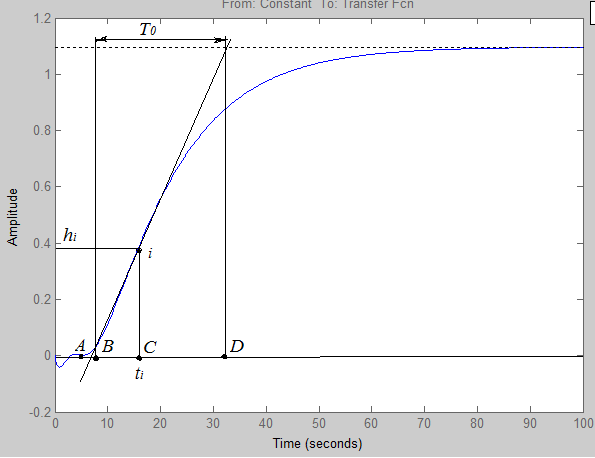
Рисунок 26 – Определение параметров ТОУ по переходной характеристике

Статический коэффициент усиления К модели ТОУ можно вычислить как по формуле (8), так и с помощью встроенной команды MatLab:

>> k=dcgain(Ws)

k = 1.0964

Время запаздывания τ определяем по диаграмме переходной характеристики непрерывной модели (рис.26), полученной в процессе идентификации. На графике находим точку соответствующую максимальной скорости изменения входной величины, т.е. точку перегиба (смена знака кривизны) кривой и проводим касательную к диаграмме. Отрезок времени до от 0 до точки В (рис. 24) является временем запаздывания τ, состоящим из транспортного запаздывания τ_тр и емкостного запаздывания τ_е .

.

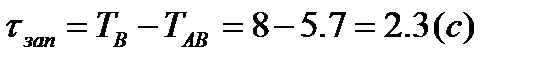Для расчета постоянной времени Т объекта управления воспользуемся табличным значением (табл. 3) соотношения 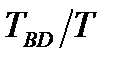=3,695 для системы третьего порядка и измеренной длиной интервала BD:

.

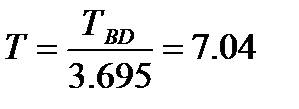Таким образом, модель исследуемого статического объекта, представленная в виде типовых динамических звеньев, запишется следующим образом:

.

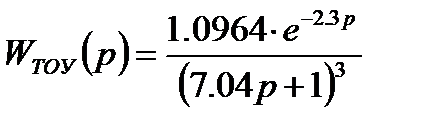Для проверки адекватности полученной передаточной функции построим график переходного процесса в приложении Simulink (рис. 27):

Рисунок 27 – Структурно-математическая схема ТОУ в обозначениях Simulink

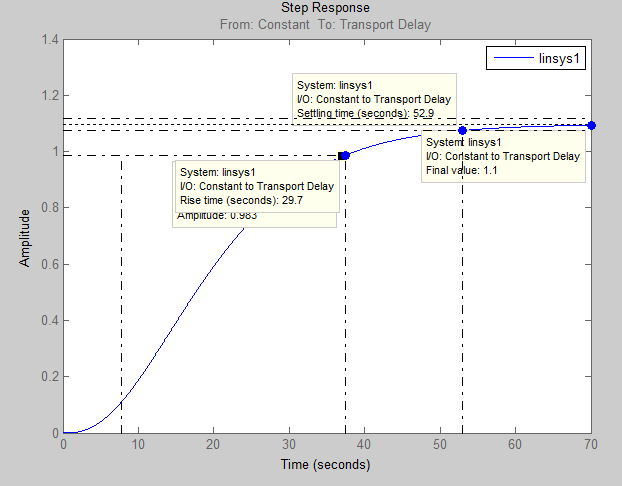
Рисунок 28 – Переходная характеристика модели ТОУ аппроксимированная в виде n последовательных апериодических звеньев

Значения критериев качества в соответствии с полученной кривой разгона (рис.28) для аппроксимированной модели технологического объекта управления в виде n последовательных звеньев составят:

- время нарастания (Rise time) – 29,7 с;

- переходного процесса (Setting time) – 52,9 с;

- установившееся значение выходной величины (Final value) – 1,1 с;

- пиковая амплитуда (Peak amplitude) – 1,1;

- перерегулирование (Overshoot) – 0%;

- статическая ошибка – 10%.