Алгоритм перехода к комплексному методу

1. Заменить мгновенные значения ЭДС, напряжений и токов расчетной схемы на их комплексные изображения.

2. Заменить параметры пассивных элементов.

3. Рассчитать одним из методов расчета цепей комплексные значения искомых величин.

4. При необходимости перейти к мгновенным значениям искомых величин.

Комплексное сопротивление и проводимость. Законы Ома

И Кирхгофа в комплексной форме. Векторные

Топографические диаграммы

Рассмотрим участок цепи при последовательном соединении активного сопротивления, индуктивности и конденсатора (рис.2.7). В схеме протекает синусоидальный ток .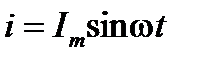

Рис. 2.7

В соответствии со вторым законом Кирхгофа (2.7) уравнение для мгновенных значений напряжений:

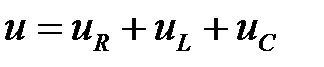; (2.13)

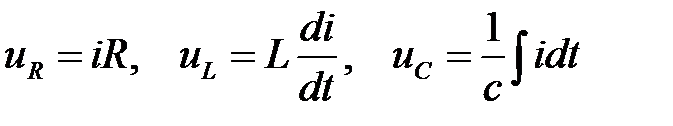. (2.14)

Подставим выражения (2.14) в уравнение (2.13). Получим:

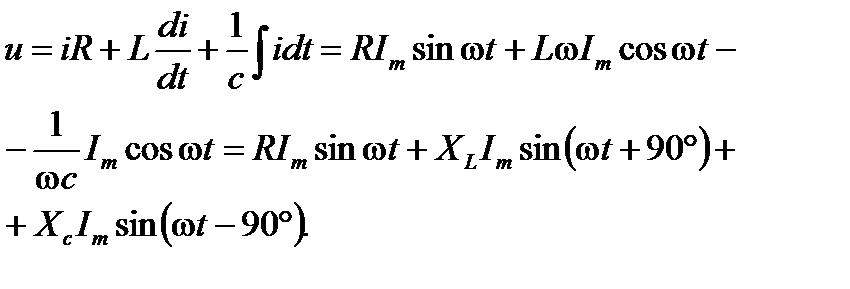(2.15)

Из выражения (2.15) следует, что напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90^o, напряжение по емкости отстает по фазе от тока на 90^o.
Запишем уравнение (2.15) в комплексной форме:

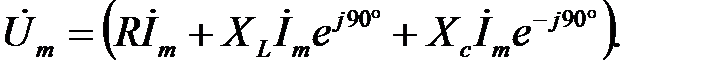(2.16)

Получим уравнение для комплексов действующих значений токов и напряжений, разделив члены (2.16) на :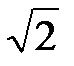

.

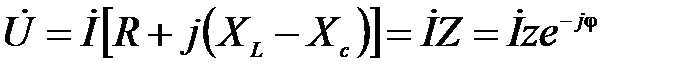Отсюда закон Ома для RLC цепи в комплексной форме

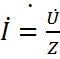(2.17) , где Z – комплексное сопротивление цепи

Откуда (2.17) отношение комплексного напряжения к комплексу тока

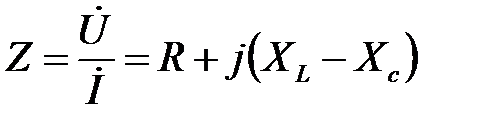. (2.18)
Точку только над комплексными величинами, отображающими синусоидальные функции времени. Комплексное число Z (2.18) может быть представлено в показательной или алгебраической форме:

(2.19)

где z- модуль комплексного сопротивления или полное сопротивление цепи;

φ- аргумент комплексного сопротивления, 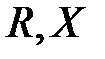- соответственно активное и реактивное сопротивление.

Для рассматриваемой схемы (рис.2.9) данные величины равны:

φ=arctg , ,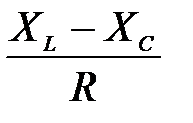

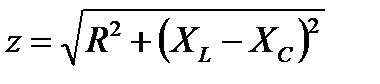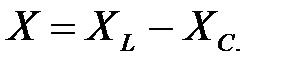(2.20)

Знак величины реактивного сопротивления X и аргумента (фазы) 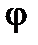зависит от соотношения индуктивного и емкостного сопротивлений.

При построении векторных диаграмм цепи возможны три режима.

1. Индуктивное сопротивление больше емкостного, величина реактивного сопротивления X и аргумента φ положительны. Цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор тока отстает от вектора напряжения на входе схемы (рис.2.8).

2. Индуктивное сопротивление меньше емкостного, величина реактивного сопротивления X и аргумента φ отрицательны. Цепь носит емкостной характер. Вектор тока опережает вектор напряжения на входе схемы (рис.2.9).

3. Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонанса напряжения (рис.2.10), который рассматривается в п.2.6.

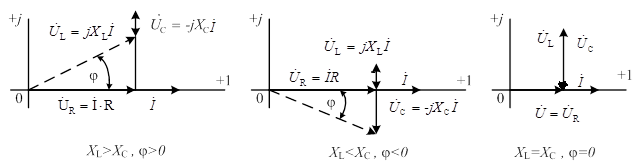
Рис. 2.8 Рис. 2.9 Рис. 2.10

В ветвях цепи при параллельном соединении активного сопротивления, индуктивности и конденсатора (рис.2.11) удобнее выполнять расчеты с использованием комплексной проводимости.

Рис. 2.11

Отношение комплексного тока к комплексному напряжению, т.е. величину обратную комплексному сопротивлению, называют комплексной проводимостью:

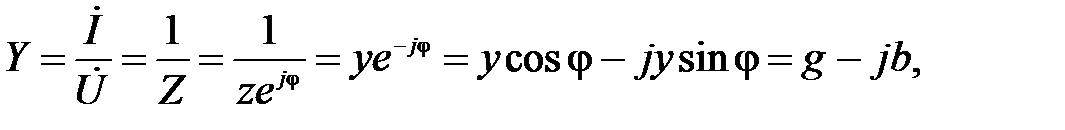(2.21)

где g, b, y - активная, реактивная и полная проводимости цепи.

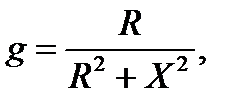
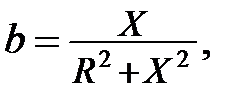
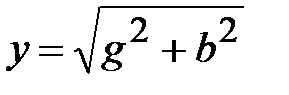. (2.22)

Единица комплексной проводимости – См (Ом ^-1).

Определим ток на входе схемы (рис. 2.11), считая, что на входе подключено синусоидальное напряжение .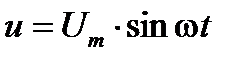

В соответствии с первым законом Кирхгофа для мгновенных значений токов:

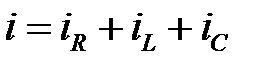, (2.23)

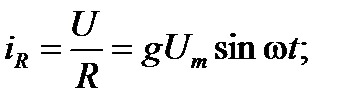
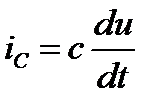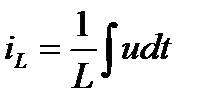, . (2.24)

Подставим выражения (2.24) в уравнение (2.23):

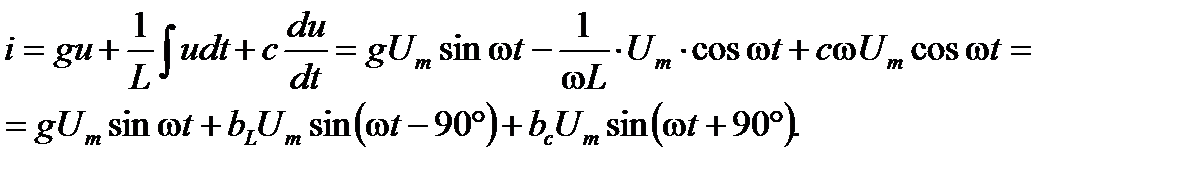(2.25)

Из уравнения (2.25) следует, что ток в ветви с индуктивностью отстает по фазе от напряжения на 90^o, ток в ветви с активным сопротивлением совпадает по фазе с напряжением, ток в ветви с емкостью опережает по фазе напряжение на 90^o.

Запишем уравнение (2.25) в комплексной форме для действующих значений токов и напряжений с учетом значений проводимостей (2.22):

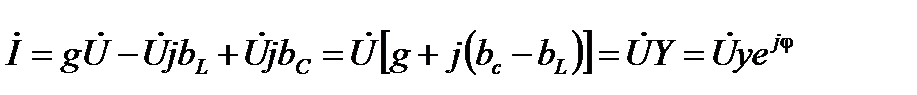. (2.26)

Знак величины реактивной проводимости b и аргумента (фазы) φ зависит от величины реактивного сопротивления X. Если X положительно, то b также положительно, если X отрицательно - b отрицательно.

При построении векторных диаграмм цепи возможны три режима.

1. Реактивная проводимость отрицательна, величина реактивного сопротивления X и аргумента φ также отрицательны. Цепь носит емкостный характер. Вектора токов через индуктивность и емкость направлены в противоположные стороны, частично компенсируя друг друга. Вектор тока опережает вектор напряжения на входе схемы (рис.2.12).

2. Реактивная проводимость положительна, величина реактивного сопротивления X и аргумента φ также положительны. Цепь носит индуктивный характер. Вектор тока отстает от вектора напряжения на входе схемы (рис.2.13).

3. Реактивная проводимость равна нулю. Вектора токов через индуктивность и емкость направлены в противоположные стороны, компенсируя друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонанса тока (рис.2.14).

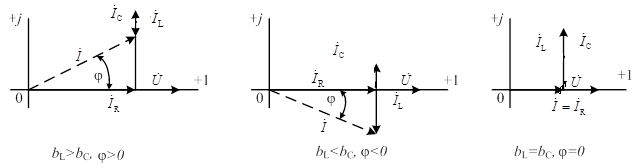
Рис. 2.12 Рис. 2.13 Рис. 2.14

Из (2.20) следует, что модуль комплексного сопротивления можно представить как гипотенузу прямоугольного треугольника, один катет которого равен активному сопротивлению R, другой реактивному сопротивлению X (рис.2.15). Аналогично из (2.22)модуль комплексной проводимости является гипотенузой прямоугольного треугольника, один катет которого равен активной проводимости g, другой реактивной проводимости b (рис.2.16).

Рис. 2.15 Рис. 2.16

Графическая интерпретация связи между модулем полного сопротивления, активным и реактивным сопротивлениями цепи в виде прямоугольного треугольника сопротивлений аналогична графической интерпретации связи между модулем полной проводимости и ее активной и реактивной составляющими.

Комплексные уравнения (2.20) и (2.28) представляет собой выражения закона Ома в комплексной форме:

.

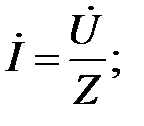
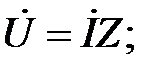
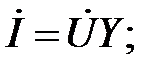
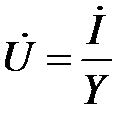Законы Кирхгофа в комплексной форме для действующих значений токов и напряжений формулируются соответственно уравнениям для мгновенных значений (2.3), (2.4).

Алгебраическая сумма комплексных значений токов в узле равна нулю (первый закон Кирхгофа)

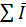=0 (2.27)

Алгебраическая сумма комплексных значений ЭДС всех источников напряжения в замкнутом контуре равна алгебраической сумме комплексных напряжений на элементах этого контура (второй закон Кирхгофа)

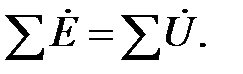(2.28)

.

В соответствии с первым законом Кирхгофа алгебраическая сумма комплексных значений токов в любом узле на комплексной плоскости должна иметь вид замкнутого многоугольника векторов токов или многолучевую звезду, сумма векторов которых равна нулю.

В соответствии со вторым законом Кирхгофа алгебраическая сумма комплексов падений напряжения и ЭДС на комплексной плоскости также должна иметь представление в виде замкнутого многоугольника векторов.

Для анализа и расчета разветвленных электрических цепей постоянного тока ранее рассмотрен ряд методов, позволяющих уменьшить порядок системы алгебраических уравнений по сравнению с методом непосредственного использования законов Кирхгофа. К ним относятся методы контурных токов, узловых потенциалов, двух узлов, эквивалентного генератора. Окончательные расчетные формулы этих методов получают в результате использования первого и второго законов Кирхгофа.

Указанные законы в комплексной форме справедливы для цепей синусоидального тока (2.27), (2.28). Поэтому в разветвленной электрической цепи, не имеющей элементов со взаимоиндуктивной связью, все расчетные уравнения для перечисленных методов (контурных токов, узловых потенциалов, двух узлов, эквивалентного генератора) справедливы для цепей синусоидального тока при условиях замены постоянных ЭДС, напряжений и токов (E, U, I ) комплексами их действующих значений ( 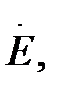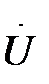, 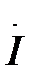), проводимости и сопротивления (g, R) – комплексными проводимостями и сопротивлениями (Y, Z). При этом алгебраическая система уравнений заменяется системой комплексных уравнений.

Расчет электрических цепей синусоидального тока при наличии в них элементов со взаимоиндуктивной связью имеет ряд особенностей, которые заключаются в учете напряжений взаимоиндукции, а также в развязывании индуктивных связей. ( См. приложение 2)