Аппроксимация модели методом В. Я. Ротача
Рассмотрим аппроксимацию модели объекта в виде последовательного соединения апериодических звеньев и звена запаздывания с обобщенной передаточной функцией вида [12]:
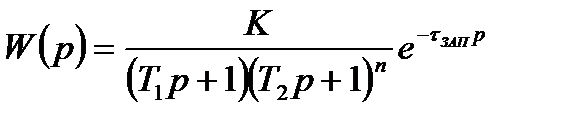 (13)
(13)
где Т1 и Т2 – постоянные времени, 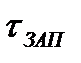 – время запаздывания, n – порядок системы, k – коэффициент передачи объекта.
– время запаздывания, n – порядок системы, k – коэффициент передачи объекта.
Критериями приближения модели к рассматриваемому реальному объекту принимаются требования совпадения переходных характеристик модели hМ(t) и реального объекта h(t) в точках t=0, t→∞, а также вточке перегиба ti, которая определяется из условия:
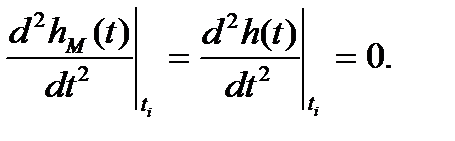
Причем в точке перегиба ti указанные характеристики должны иметь и одинаковый наклон. Сформулированные требования представим в виде системы уравнений:
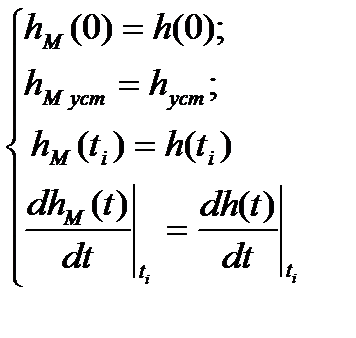 (14)
(14)
Для определения производной 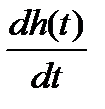 переходной характеристики h(t) вточке, где эта характеристика имеет максимальный наклон проводят касательную и находят длину отрезка То (рис. 27).
переходной характеристики h(t) вточке, где эта характеристика имеет максимальный наклон проводят касательную и находят длину отрезка То (рис. 27).
Учитывая введенные на рис. 29 обозначения критерии приближения модели к рассматриваемому объекту (14) запишем следующим образом:
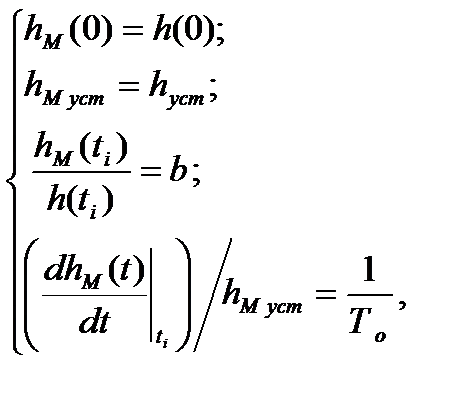 (15)
(15)
где 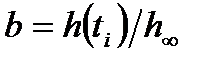 .
.
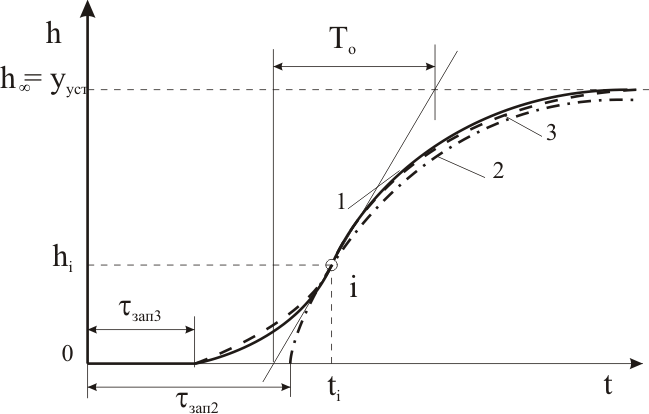
Рисунок 29 – Аппроксимация промышленного объекта упрощенными моделями с использованием метода В. Я. Ротача: 1 – экспериментальная переходная характеристика объекта; 2 – переходная характеристика модели (первого порядка) объекта;
3 – переходная характеристика модели (второго порядка) объекта
Рассмотрим аппроксимацию технологического объекта математическими моделями первого и второго порядка.
1. Аппроксимация объекта моделью, состоящей из статического апериодического звена первого порядка извена запаздывания:
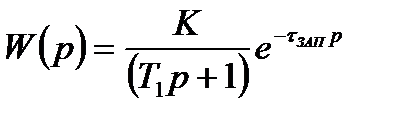 .
.
Значение коэффициента передачи звена равна установившемуся значению переходной функции: 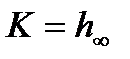 . Два последних требования из системы уравнений (15) запишем, как:
. Два последних требования из системы уравнений (15) запишем, как:
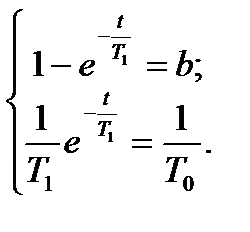 (16)
(16)
Из выражения (16) рассчитаем постоянную времени Т1 модели объекта 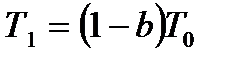 и момент времени, при котором выполняется условие аппроксимации:
и момент времени, при котором выполняется условие аппроксимации:
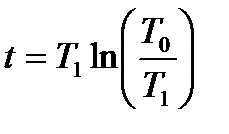 .
.
Затем, по известному значению ti, определяется время запаздывания:
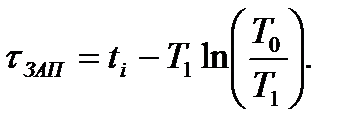
Переходная характеристика hМ(t) модели изображена на рис. 29 пунктирной кривой (2).
На практике, в качестве постоянной времени T1 принимают величину Т0, а время запаздывания τЗАП принимают равным τЗАП3. Подобное упрощение допускается лишь при малых значениях b (b<0.05).
2. Аппроксимация объекта моделью, состоящей из последовательно соединенных двух апериодических звеньев и звена запаздывания:
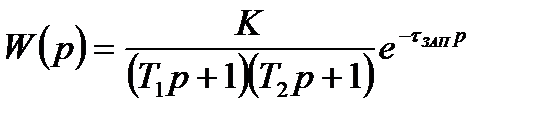 .
.
Переходная характеристика без учета звена запаздывания может быть определена из таблицы преобразования Лапласа следующим образом:
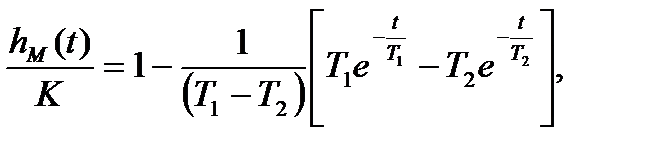 (17)
(17)
Выражение для первой и второй производных переходной функции по времени получим как:
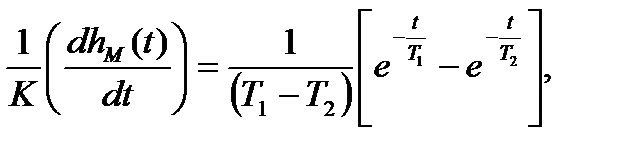 (18)
(18)
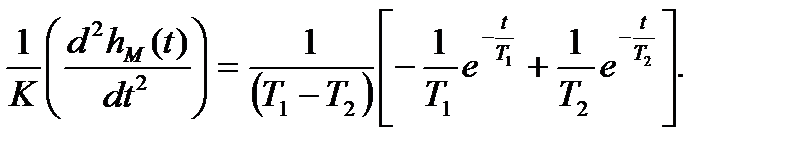 (19)
(19)
Для того, чтобы определить координаты точки перегиба i приравняем к нулю выражение (19) для второй производной переходной функции:
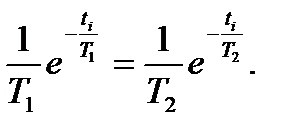 (20)
(20)
Выразив из уравнения (20) 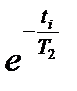 и подставив в формулы (17) и (18), получим систему уравнений вида:
и подставив в формулы (17) и (18), получим систему уравнений вида:
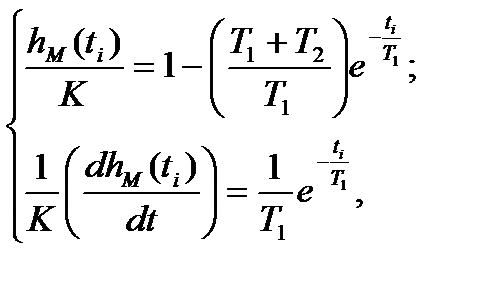 (21)
(21)
Введем безразмерные переменные 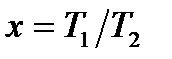 и
и 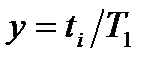 и перепишем формулы (20) и (21) как:
и перепишем формулы (20) и (21) как:
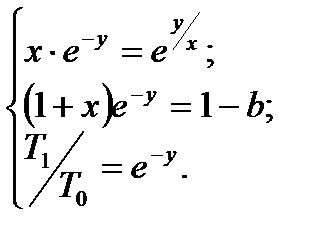 (22)
(22)
Решая систему трансцендентных уравнений (22) при известных значениях Т0 и b, определим параметры модели T1, T2 и ti. Если при этом окажется, что найденная координата аппроксимирующей модели ti меньше значения ti, рассчитанного по графику переходной характеристики, то следует ввести время запаздывания:
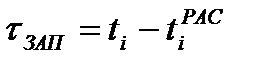 .
.
Аппроксимация объекта моделью второго порядка допустима лишь при b<0.265. Это предельное значение b для апериодического звена второго порядка, которое наступает при T1=T2.
Вычисления параметров моделей для любого порядка n производятся аналогично. На практике оказывается достаточным выбирать n<4, что соответствует b<0.371. Выше приведенные расчеты параметров модели удобно проводить с помощью номограммы (рис. 30).
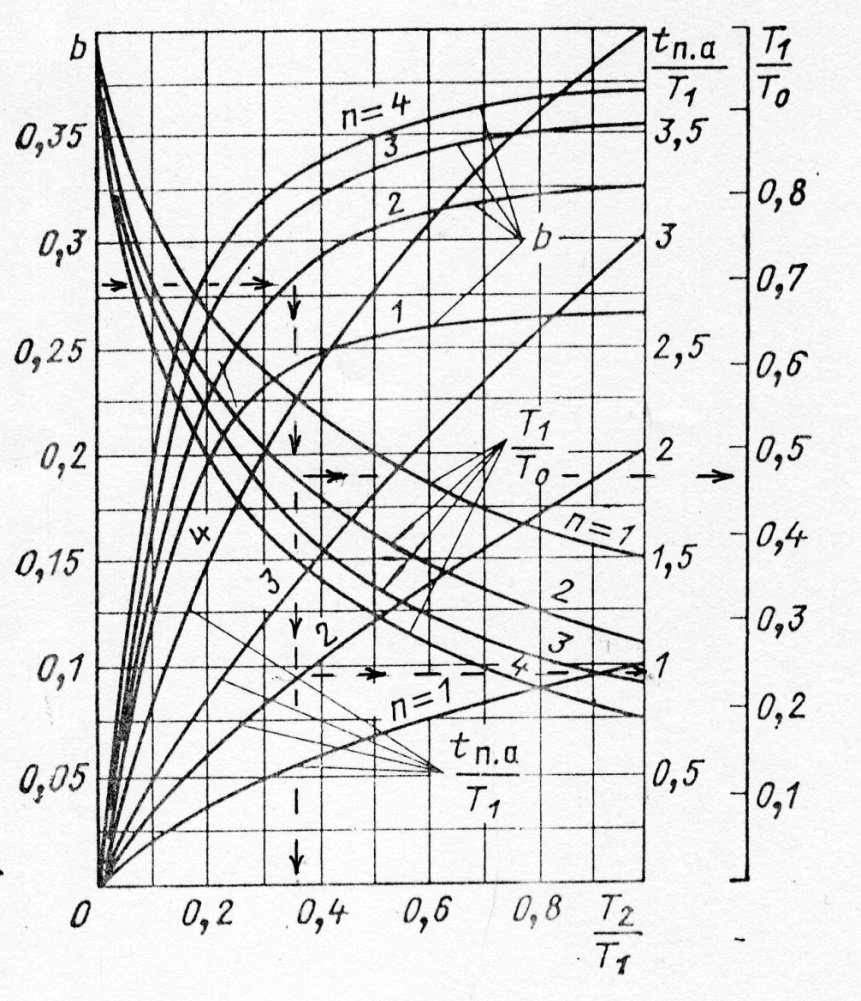
Рисунок 30 – Номограмма для определения параметров объектов [14]
Порядок нахождения параметров модели с использованием номограммы состоит в следующем:
1. По экспериментальной переходной характеристике 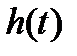 определяются значения
определяются значения 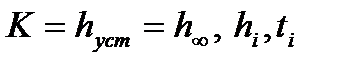 и
и 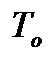 .
.
2. В зависимости от значения 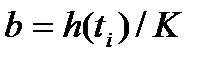 выбирается порядок модели n.
выбирается порядок модели n.
3. По номограмме, для полученных b и n, определяются отношения 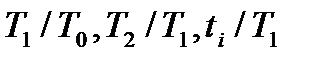 , знание которых позволяет вычислить параметры модели: T1, Т2 и ti, а также
, знание которых позволяет вычислить параметры модели: T1, Т2 и ti, а также 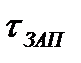 .
.
Определим параметры модели исследуемого технологического объекта – ресивера. Исходные данные для выбранной точки перегиба по переходной характеристике (рис. 26) с координатами 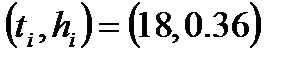 следующие:
следующие:
К=1.1, 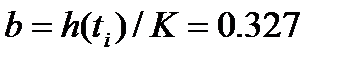 (соответствует BD) .
(соответствует BD) .
По номограмме (рис. 30) для уровня b=0.327 выбираем кривую соответствующую минимальному порядку системы n=3, и соотношение параметров модели объекта:
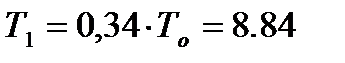 ,
, 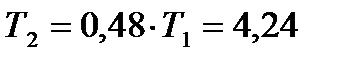 ,
, 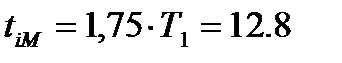 .
.
Таким образом, передаточная функция модели технологического объекта запишется в виде:
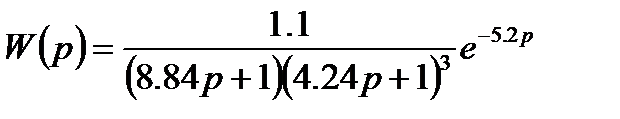
Структурная схема технологического объекта управления с учетом принятой структуры и рассчитанных значений параметров показана на рис. 31.

Рисунок 31 – Структурная схема модели объекта, аппроксимированная по методу В.Я. Ротача
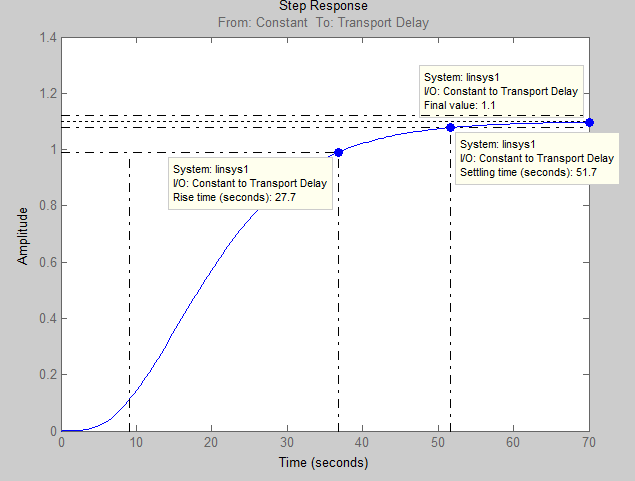
Рисунок 32 – Переходная характеристика модели ТОУ аппроксимированная по методу В. Я. Ротача
По переходной характеристике (рис.32), полученной для аппроксимированной модели объекта методом В.Я.Ротача
- время нарастания (Rise time) – 27,7 с;
- переходного процесса (Setting time) – 51,7с;
- установившееся значение выходной величины (Final value) – 1,1 с;
- пиковая амплитуда (Peak amplitude) – 1,1;
- перерегулирование (Overshoot) – 0%;
- статическая ошибка – 10%.
Для проведения сравнительного анализа адекватности расчетных моделей графики кривых разгона для моделей технологического объекта управления полученной в результате идентификации, а также аппроксимации представлены на рис. 33.
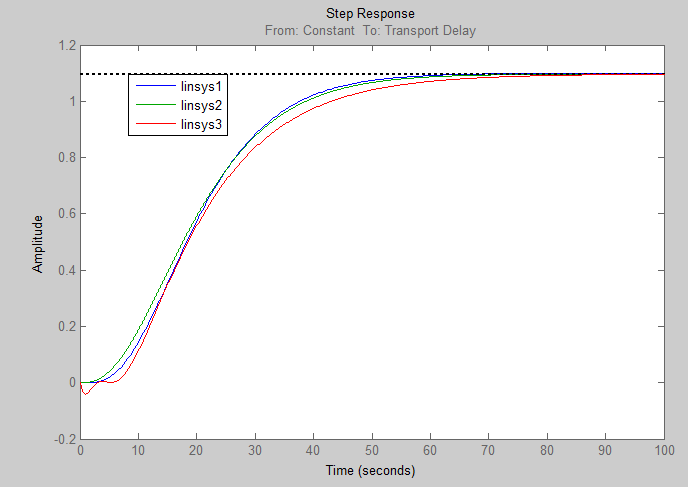
Рисунок 33 – Сравнительный анализ аппроксимированных моделей и модели, полученной в результате идентификации:
linsys1 – 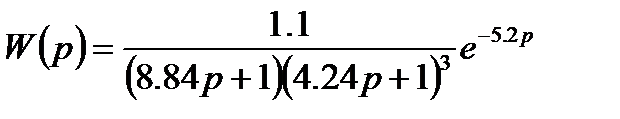 ; linsys2 –
; linsys2 – 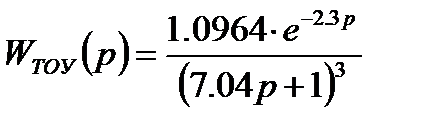 ; linsys3 –
; linsys3 – 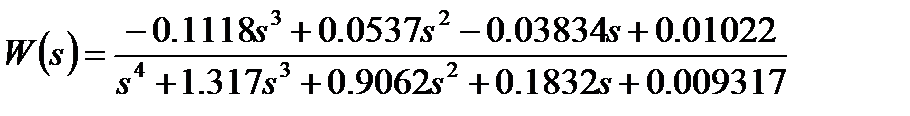
Критерий приближения (по контрольным точкам) модели к рассматриваемому объекту выполняется как для диаграммы (linsys1), так и для диаграммы (linsys2). Поскольку порядок модели linsys2, полученной по переходной характеристике, ниже, чем в других моделях, что упростит дальнейшую настрой регулятора, то целесообразно в качестве расчетной использовать передаточную функцию вида:
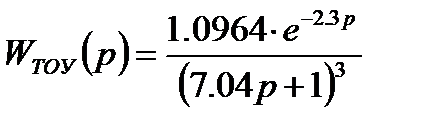 .
.
Дата добавления: 2021-05-28; просмотров: 838;











