Квадратичное аппроксимирование обобщенными полиномами

Рассмотрим два варианта метода наименьших квадратов с обобщенными полиномами в качестве аппроксимирующей функции: а) исходная функциональная зависимость задана таблицей; б) исходная функциональная зависимость задана непрерывной функцией.

а) Точечное квадратичное аппроксимирование.

Пусть исходная функция задана таблицей {x_k , y_k}, k=0,...,n. Потребуем, чтобы квадратичное отклонение

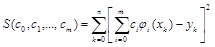
было минимальным.

Поскольку здесь параметры 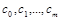выступают в роли независимых переменных функции S, то ее минимум найдем, приравнивая нулю частные производные по этим переменным:

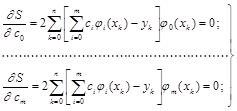. (2.13)

Введем обозначения:

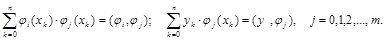
Тогда систему (2.13) можно записать в виде:

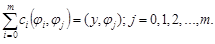(2.14)

Система (2.14) представляет собой систему (m+1) линейных алгебраических уравнений относительно неизвестных коэффициентов с_i. Определитель этой системы симметричен относительно главной диагонали:

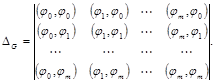
Он называется определитель Грама системы функций j₀, j₁,..., j_m.

Можно показать, что определитель Грама равен нулю тогда и только тогда, когда система функций j₀, j₁,..., j_m линейно зависима[11], то есть в этом случае система уравнений не имеет решения [2].

Наиболее просто система (2.14) решается в случае, когда выбранная система функций {j_i(x)} – ортогональная, то есть когда

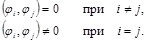
В этом случае в определителе Грама отличны от нуля только элементы главной диагонали и решение системы (2.14) сразу записывается в виде:

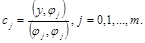
Отметим, что если система функций ортогональная, то она линейно независима, то есть решение системы (2.14) всегда существует.

Примечание 2. Метод получения ортогональных многочленов (процесс ортогонализации Шмидта).

Рассмотрим способ получения системы ортогональных многочленов на заданной таблице {x_k, y_k}, k=0, 1, ..., n.

Положим j₀(х)=1, j₁(х)=х – a₁. Потребуем выполнения условия ортогональности для этих функций:

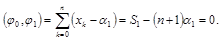
Первое условие выполняется автоматически, а из второго находим

,

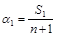то есть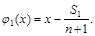Проверка показывает, что многочлены j₀, j₁ – ортогональны:

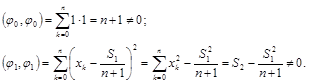
Многочлены более высоких степеней можно получить по рекуррентной формуле:

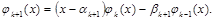(2.15)

Выражения для коэффициентов a_k+1 и b_k+1 также находятся из условия ортогональности.

Предположим, что уже построены ортогональные многочлены j₀(х), j₁(х), ..., j_k(x). Потребуем, чтобы (j_k+1,j_k)=0; (j_k+1,j_k–1)=0.

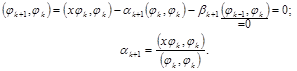
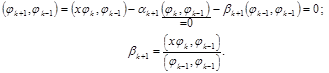
Ортогональность построенного многочлена j_k+1(х) всем многочленам j_i(x) (i £ k–2) следует из (2.15):

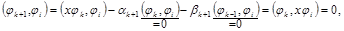
так как степень многочлена хj_i £ k–1.

Конец примечания 2.

б) Интегральное квадратичное аппроксимирование.

Пусть исходная функция задана на [a, b] в виде некоторой непрерывной функции y=f(x). В этом случае в качестве меры отклонения используется интегральное квадратичное отклонение

,

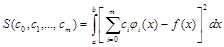и так же, как и в предыдущем случае, коэффициенты аппроксимирующего многочлена подбирают таким образом, чтобы это отклонение S имело минимальное значение.

Система уравнений для определения коэффициентов с_i имеет вид:

.

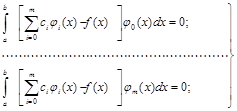С обозначениями

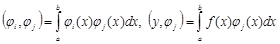
система примет вид (2), и все суждения об этой системе, приведенные выше, сохраняют силу.

Условие ортогональности для непрерывных функций будет иметь интегральный вид:

,

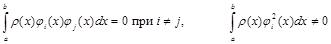где r(х) – весовая функция.

Например, на отрезке [–1;1] с единичной весовой функцией ортогональными являются полиномы Лежандра:

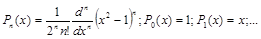(2.16)

Рекуррентная формула:

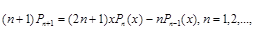
то есть .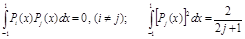

Рассмотренные ранее полиномы Чебышева ортогональны на [a,b] c весовой функцией r(x)=1/(1 – x²)^1/2 , то есть

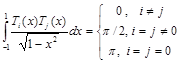
Поэтому, если аппроксимирующую функцию построить, взяв в качестве базисных функций, например, полиномы Лежандра

,

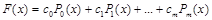то ее коэффициенты можно определить по формуле

,

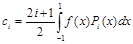где f(x)– аппроксимируемая функция.