ИНТЕРПОЛЯЦИОННЫЙ ПОЛИНОМ НЬЮТОНА
Пусть х0, х1,..., хn – произвольные попарно не совпадающие узлы, в которых известны значения функции f. Запишем полином степени n в виде
Nn(x)=A0+A1(x–x0)+ A2(x–x0)(x–x1)+...+An(x–x0)(x–x1)...(x–xn–1).
Если выполняются условия (2.4)
Nn(xi)=f(xi), i=0, 1, ..., n,
то полином будет интерполяционным. Его коэффициенты найдутся из этих условий.
Положим х=х0, тогда f(x0)=A0. Коэффициент А0 определен.
Положим х=х1, тогда f(x1) =f(x0)+A1(x1–x0).
Отсюда 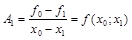 . Этот коэффициент называется разделенной разностью первого порядка. При малом расстоянии между узлами х1 и х0 величина f(x0; x1) близка к первой производной функции f(x).
. Этот коэффициент называется разделенной разностью первого порядка. При малом расстоянии между узлами х1 и х0 величина f(x0; x1) близка к первой производной функции f(x).
Положим х=х2 , тогда f(x2)= f(x0)+f(x0; x1)(x2–x0)+A2(x2–x0)(x2–x1).
Отсюда 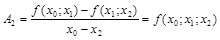 ,
,
где 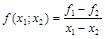 .
.
Величина f(x0; x1; x2) называется разделенной разностью второго порядка, и при малом расстоянии между х0, х1, х2 она близка ко второй производной функции f(x).
Аналогично находятся все остальные коэффициенты:
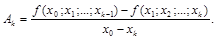
Полином вида
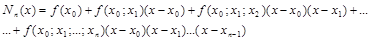
называется интерполяционным полиномом Ньютона для неравных промежутков. Он тождественно совпадает с интерполяционным полиномом Лагранжа, так что все суждения о погрешности Ln(x) остаются в силе и для Nn(x).
Сравним эти две формы интерполяционных полиномов.
Полином Лагранжа явно зависит от каждого значения функции fi,поэтому при изменении n полином требуется строить заново. Полином Ньютона выражается не через значения функции f, а через ее разделенные разности. При изменении n у него требуется только добавить или отбросить соответствующее число стандартных слагаемых. Поэтому интерполяционный полином Ньютона удобнее использовать, когда интерполируется одна и та же функция, но число узлов может меняться. Если же узлы фиксированы и интерполируется не одна, а несколько функций, то удобнее пользоваться интерполяционным полиномом Лагранжа.
Кроме того, в формуле Ньютона безразличен порядок, в котором пронумерованы узлы интерполяции. Это дает возможность подключать (или убирать) любые узловые точки в процессе построения интерполяционного полинома, причем в произвольном порядке. Пусть, например, необходимо вычислить значение функции в точке х, лежащей между узловыми точками х8 и х9некоторой таблицы. Перенумеровываем таблицу: х9« х0 ; х8 « х1 ; х10 « х2 ; х7 « х3 ; и так далее. Одновременно начинаем строить почленно интерполяционный полином Ньютона и вычислять значение f(x) с необходимой точностью.
Рассмотрим частные случаи интерполяционного многочлена Ньютона для таблиц с постоянным шагом.
1. Интерполяционный полином Ньютона для интерполирования вперед.
Пусть xi = x0+ih, h > 0, i = 0, 1,..., n.
Введем новую переменную t=(x – x0)/h.
Тогда x – x0 = t×h, x – x1 = (t – 1)×h, ..., x – xk = (t – k)×h и интерполяционный полином Ньютона можно записать в виде
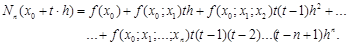
Назовем D1yk = yk+1 – yk конечной разностью первого порядка, D2yk=Dyk+1 – D yk - конечной разностью второго порядка, ...,
Dnyk=Dn–1yk+1 – Dn–1yk - конечной разностью n-ого порядка.
Здесь уk = f(xk).
Конечные разности обладают следующими свойствами:
1) связь с производными: Dnyk » hnf(n)(x), в частности для полиномов Dnyk = anhnn!;
2) связь со значениями функции: 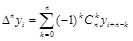 , (2.7)
, (2.7)
где 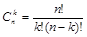 – коэффициенты бинома Ньютона;
– коэффициенты бинома Ньютона;
3) связь с разделенными разностями: 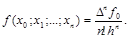
Тогда интерполяционный полином Ньютона можно переписать в виде
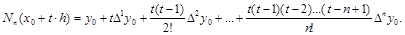 Остаточный член этой интерполяционной формулы имеет вид:
Остаточный член этой интерполяционной формулы имеет вид:
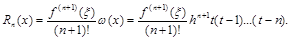
Видно, что с точки зрения уменьшения погрешности, целесообразно ограничиться случаем t<1, то есть использовать эту формулу при х0<x<x1 .
Для других значений аргумента, например для х1<x<x2,лучше взять в качестве начального значения х1 и так далее.
Таким образом, можно записать
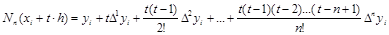 ,
,
где 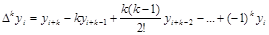 ; i=0, 1, 2,...
; i=0, 1, 2,...
Это первый интерполяционный полином Ньютона для интерполирования вперед. Его обычно используют для вычисления значений табличной функции в точках левой половины рассматриваемого отрезка, а также для экстраполяции влево (при t<0).
2. Интерполяционный полином Ньютона для интерполирования назад.
Для правой половины рассматриваемого отрезка разности лучше вычислять справа налево. Тогда t=(x – xn)/h , –1<t<0и
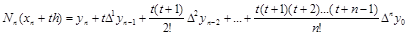 Здесь xn–1<x<xn .
Здесь xn–1<x<xn .
Аналогично предыдущему можно записать
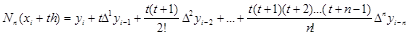 i=n, n–1, n–2,...
i=n, n–1, n–2,...
Это второй интерполяционный полином Ньютона для интерполирования назад. Используется для вычисления значений табличной функции в точках правой половины рассматриваемого отрезка, а также для экстраполяции вправо.
Пример. Построить интерполяционный полином, если задана следующая таблица:
| xк | yк | D1y | D2y0 | D3y0 |
1. Интерполяционный полином Лагранжа
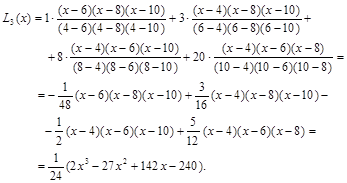
2. Интерполяционный полином Ньютона.
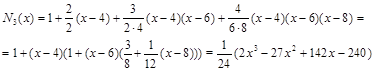
3. Интерполяционный полином Ньютона для интерполирования вперед. t=(x – 4)/2.
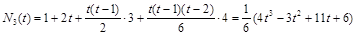 .
.
4. Интерполяционный полином Ньютона для интерполирования назад. t=(x – 10)/2.
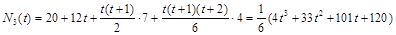 .
.
Дата добавления: 2020-10-25; просмотров: 809;











