Алгоритм методу добутків
У перший стовпчик таблиці записують рівновіддалені варіанти xi вибірки, розміщуючи їх у зростаючому порядку.
У другий стовпчик таблиці записують відповідні частоти ki варіант. Суму усіх елементів цього стовпчика (об’єм вибірки) записують у останню клітинку цього стовпчика.
Третій стовпчик містить умовні варіанти ui вибірки. Для знаходження умовних варіант вибірки треба:
a) значення варіанти вибірки з найбільшою частотою (моду) С обрати за умовний нуль;
b) знайти різницю h між будь-якими двома сусідніми варіантами;
c) обчислити умовні варіанти ui за формулою 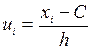 .
.
У четвертий стовпчик записують добутки частот та відповідних умовних варіант ui∙ ki. Суму елементів стовпчика записують в останню клітинку цього стовпчика.
Знаходять добутки частот та квадратів умовних варіант ui∙ ki2 і записують їх у п’ятий стовпчик. Суму елементів стовпчика записують в останню клітинку цього стовпчика.
Знаходять добутки частот та квадратів умовних варіант, збільшених на одиницю, ki (ui+1)2 і записують їх у шостий стовпчик. Суму елементів стовпчика записують в останню клітинку цього стовпчика.
Перевіряють обчислення так: сума елементів шостого стовпчика повинна задовольняти тотожність 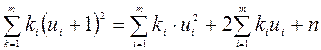
Обчислюють умовні моменти за формулами
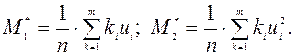
Обчислюють вибіркові середню та дисперсію за формулами
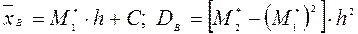
Приклад.Знайти методом добутків вибіркові середню та дисперсію заданої вибірки
| xi | 18,6 | 19,4 | 19,8 | 20,2 | 20,6 | |
| ki |
У даному випадку: варіанти вибірки рівновіддалені
h=x2–x1=19-18,6=0,4; найбільша частота 40 у варіанти 19,8. Тому умовним нулем буде С=19,8.
| хі | ki | ui | ui∙ ki | ui∙ ki2 | ki (ui+1)2 |
| 18,6 | -3 | -12 | |||
| -2 | -12 | ||||
| 19,4 | -1 | -30 | |||
| 19,8 | |||||
| 20,2 | |||||
| 20,6 | |||||
| п=100 | ∑=-32 | ∑=116 | ∑=152 |
Для контролю перевіряємо умову:
116+2∙(–32)+100=152; 152º152.
Знайдемо умовні моменти
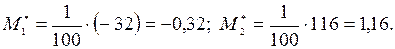
Знаходимо шукані вибіркову середню та вибіркову дисперсію
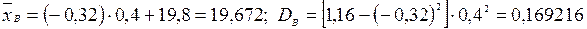
Дата добавления: 2022-02-05; просмотров: 840;











