НЕЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ
Рассмотрим нелинейные быстроменяющиеся функции. Пусть дана таблица значений некоторой функции y=f(x) вместе с конечными разностями:
| xk | yk | Dy0 | D2y0 | D3y0 |
Пусть требуется вычислить у(0,5). Очевидно, это значение лежит в диапазоне (1;11). Используем интерполяционный полином Ньютона:
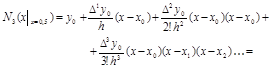
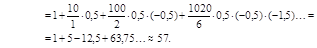
Результат весьма далек от ожидаемого, так как этот ряд содержит быстровозрастающие члены и совсем не похож на сходящийся.
Как интерполировать такие функции? Использовать более подробные таблицы? А если их нет? Универсального рецепта не существует, но для каждой конкретной функции часто удается найти свой способ интерполяции, дающий приемлемую точность.
Для этого, выяснив качественное поведение функции (или зная ее физический смысл, или сравнивая ее поведение с известными элементарными функциями), стараются подобрать такое преобразование переменных h=h(у) ; x=x(х), чтобы в новых переменных график функции h(x) мало отличался от прямой линии на протяжении нескольких шагов таблицы.
Затем составляют таблицу hi=h(xi), интерполируют по ней и обратным преобразованием находят у=у(h).Этот прием называют методом выравнивания.
В рассматриваемом примере делаем замену x=х; h=lg y и составляем новую таблицу:
| xk | hk | Dh0 | D2h0 | D3h0 |
| 1,0414 | 0,0064 | |||
| 1,0414 | 1,0414 | 0,0064 | ||
| 2,0828 | 1,0478 | |||
| 3,1306 |
Первые разности мало отличаются друг от друга – это говорит о том, что выбранная зависимость h(x) близка к линейной.
Проводим интерполяцию по интерполяционному полиному Ньютона: 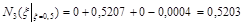 .
.
Таким образом, h=0,5203, у=100,5203 » 3,314.
Дата добавления: 2020-10-25; просмотров: 714;











