Глобальная интерполяция

В случае глобальной интерполяции отыскивается единая интерполирующая функция на всем интервале 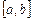. Самым распространенным способом является полиномиальная интерполяция.

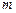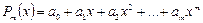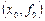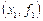Будем искать интерполирующую функцию в виде полинома (многочлена) -ой степени . Какова должна быть степень многочлена, чтобы удовлетворить всем условиям интерполяции? Допустим, что заданы две точки: и , т.е. 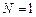. Через эти точки можно провести единственную прямую, т.е. интерполирующей функцией будет полином первой степени 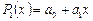. Через три точки ( 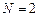) можно провести параболу 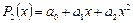и т.д. Рассуждая таким способом, можно предположить, что искомый полином должен иметь степень .

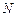Для того, чтобы доказать это, выпишем систему уравнений на коэффициенты. Уравнения системы представляют собой условия интерполяции при каждом :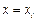

.

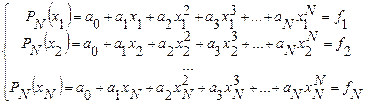
Данная система является линейной относительно искомых коэффициентов 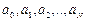_. Известно, что СЛАУ имеет решение, если ее определитель отличен от нуля. Определитель данной системы

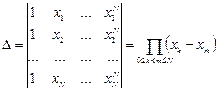
носит имя Вандермонда. Из курса математического анализа известно, что он отличен от нуля, если . В нашем случае это означает, что все узлы интерполяции различны, что верно по определению. Таким образом, доказано, что система имеет решение.

Мы показали, что для нахождения коэффициентов 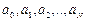надо решить СЛАУ, что является сложной задачей. Но есть другой способ построения полинома 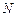-й степени, который не требует решения такой системы.

Полином Лагранжа

Решение ищем в ви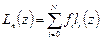де , где 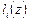– базисные полиномы 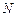-й степени, для которых выполняется условие: 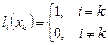. Убедимся в том, что если такие полиномы построены, то 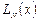будет удовлетворять условиям интерполяции: 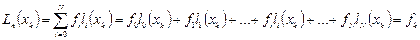Каким образом построить базисные полиномы? Определим

, .

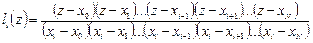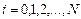Легко понять, что

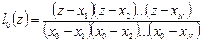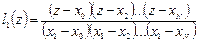, , и т.д.

Функция 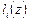является полиномом 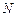–й степени от 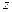и для нее выполняются условия «базисности»:

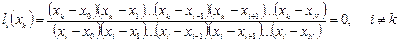, т.е. ;

.

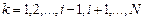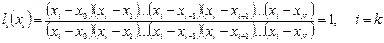Таким образом, нам удалось решить задачу о построении интерполирующего полинома 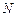-й степени, и для этого не нужно решать СЛАУ. Полином Лагранжа можно записать в виде компактной формулы: 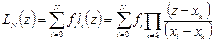. Погрешность этой формулы можно оценить, если исходная функция 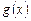имеет производные до 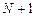порядка:

.

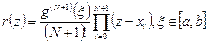Из этой формулы следует, что погрешность метода зависит от свойств функции 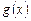, а также от расположения узлов интерполяции и точки 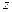. Как показывают расчетные эксперименты, полином Лагранжа имеет малую погрешность при небольших значениях 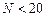. При бόльших 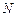погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (т.е. его погрешность не убывает с ростом ).

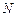Рассмотрим частные случаи. Пусть 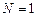, т.е. заданы значения функции только в двух точках. Тогда базовые полиномы имеют вид:

, , ,

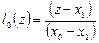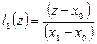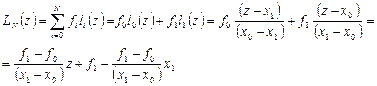т.е. получаем формулы кусочно-линейной интерполяции.

Пусть 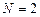. Тогда:

, , ,

.

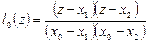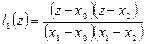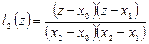В результате мы получили формулы, так называемой квадратичной или параболической интерполяции.

ПРИМЕР 3.3. Задана таблица значений функции:

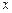
				3,5
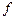
	-1	0,2	0,5	0,8

Требуется найти значение функции при 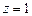, используя интерполяционный полином Лагранжа. Для этого случая 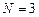, т.е. полином Лагранжа имеет третий порядок. Вычислим значения базисных полиномов при :

,

,

,

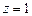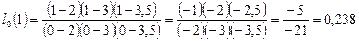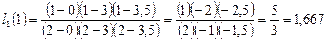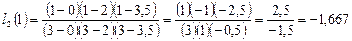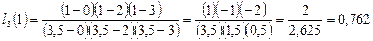
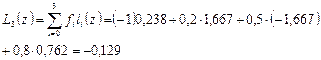
Итак, интерполирующая функция принимает в точке 1 значение -0,129.