Интерполяция при помощи полиномов Лагранжа
Воспроизводящая функция в большинстве случаев рассчитывается по формуле: 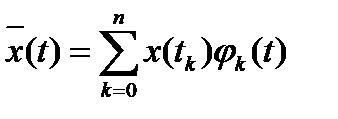 , где
, где 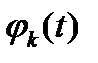 − некоторые функции. Эти функции обычно стремятся выбрать так, чтобы
− некоторые функции. Эти функции обычно стремятся выбрать так, чтобы
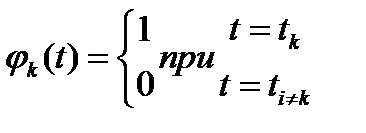 . (2.14)
. (2.14)
В этом случае 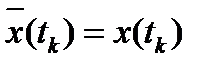 , т.е. значения воспроизводящей и исходной функций совпадают в моменты взятия отсчетов или, как принято говорить, в узлах интерполяции.
, т.е. значения воспроизводящей и исходной функций совпадают в моменты взятия отсчетов или, как принято говорить, в узлах интерполяции.
Функции, обладающие этим качеством, нашел выдающийся французский математик и механик Жозеф Луи Лагранж (1736-1813).
Функции Лагранжа L зависят от одного аргумента t и двух параметров – n и k. Здесь n – максимальный номер отсчета, а k – номер функции.
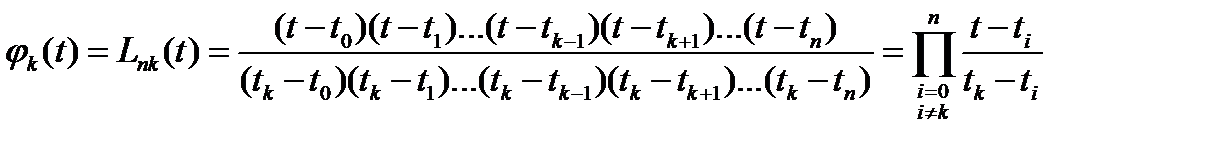 (2.15)
(2.15)
Несложно доказать, что функции Лагранжа отвечают условию (2.14). Из формулы (2.15) следует, что функция Лагранжа является полиномом n-ой степени. Воспроизводящая функция 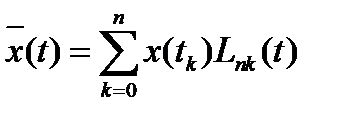 по этой причине также является полиномом и называется полиномом Лагранжа n-ой степени.
по этой причине также является полиномом и называется полиномом Лагранжа n-ой степени.
Полином Лагранжа можно использовать для расчета воспроизводящей функции как при равномерной, так и при неравномерной дискретизации. Если же ограничиться только равномерной дискретизацией, полином Лагранжа можно преобразовать к виду:
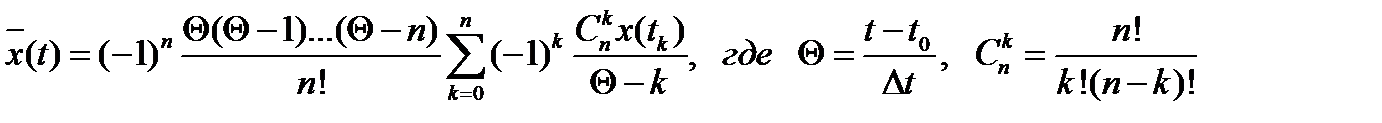
Дата добавления: 2021-04-21; просмотров: 574;











