Интерполяция сплайнами.

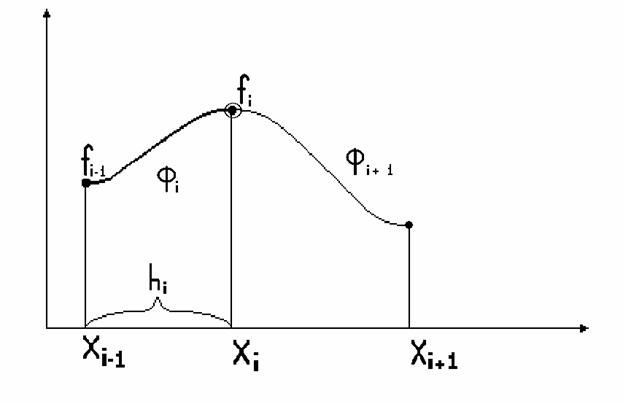
Происхождение термина “сплайны” связано с гибкой чертежной линейкой, которой пользовались для рисования гладких кривых, проходящих через заданные точки. Из теории упругости следует, что получающаяся кривая имеет постоянную кривизну и разрывы возникают лишь в третьей производной.

Обычно для сплайна выбирают кубический полином 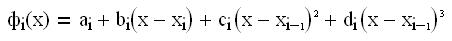, определенный на интервале х из [x_i-1, х_i].

При этом вся кривая представляет собой набор таких кубических полиномов, с определенным образом подобранными коэффициентами а_i , b_i , c_i , d_i , i- параметр сплайна.

! Если вдоль сплайна совершается механическое движение, то непрерывность второй производной предполагает непрерывность ускорения и, следовательно, отсутствие резких изменений приложенной силы.

N+1 узлов

N интервалов

4N неизвестных

Условия подбора коэффициентов:

1)условия Лагранжа: , ,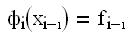

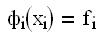
2)непрерывность первой и второй производной в узлах

ф_i’(x_i) = ф_i+1’(x_i); ф_i”(x_i) = ф_i+1(x_i)

3) условия в крайних узлах x₀ и x_n. Обычно задают условия свободных концов сплайна :

ф₁”(x₀) = 0, ф_n”(x_n) = 0

Из полученных условий определяются зависимости между коэффициентами сплайнов:

В узле х = х_i-1 коэффициент a_i = f_i-1.

В следующем узле x = x_i выполняется условие a_i+b_ih_i+c_ih_i²+d_ih_i³ = f_i, где элементарный шаг h_i = x_i – x_i-1.

Потребуем непрерывности первой и второй производной на конце интервала

ф_i^/(x) = b_i+2c_i(x-x_i-1)+3d_i(x-x_i-1)² ,

ф_i^//(x) = 2c_i+6d_i(x-x_i-1);

В узле x = x_i первая производная

ф_i^/(x_i) = b_i+2c_ih_i+3d_ih_i² (1)

ф_i+1^//(x_i) = b_i+1 (2)

Приравнивая (1) и (2), получаем b_i +2c_ih_i+3d_ih_i² = b_i+1.

Вторая производная

ф_i^//(x_i) = 2c_i+6c_ih_i (3)

ф_i+1^//(x_i) = 2c_i (4)

Приравнивая (3) и (4), получаем в свою очередь c_i+3d_ih_i = c_i+1. Таким образом стыкуем все полиномы в узлах 1 ≤ i ≤ n-1. В крайних точках диапазона

ф₁^//(x₀) = 2c₁ = 0 → c₁ = 0

ф₁^//(x_n) = 2c_n+6d_nh_n = 0 → c_n +3d_nh_n = 0

Для всех 0 ≤ i ≤ n вышеприведенные соотношения представляют собой полную систему 4n линейных алгебраических уравнений относительно коэффициентов сплайнов, которую можно привести к системе ЛАУ, выразив коэффициенты a_i, b_i, d_i через c_i и решить методом Гаусса или прогонки.

Система N линейных уравнений для коэффициентов с_i:

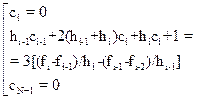
для ,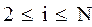

где h_i = x_i-x_i-1

После определения коэффициентов c_i , 2N коэффициентов b_i и d_i вычисляются по формулам:

,

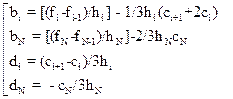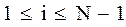
И N уравнений для ,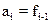

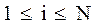
Сплайновая интерполяция хороша тем, что требует знания в узлах только значений функции, но не ее производных.