Интерполяция многочленами

В общем виде задача интерполяции многочленами формулируется следующим образом: пусть на отрезке [a, b] таблично задана функция y = f(x) в n точках, то есть заданы значения аргумента x₁, x₂, ..., x_n и известны соответствующие им значения функции y₁, y₂, ..., y_n . Требуется построить степенной полином вида

P_n(x)= a₁+ a₂x + a₃x²+ ... + a_nxⁿ ,

значения которого в точках x₁, x₂, ..., x_n совпадает со значениями табличной функции

P_n(x_i)= y_i = f(x_i).

Такой полином всегда существует и оказывается единственным. Для вычисления значений его коэффициентов можно использовать условие равенства значений полинома и таблично заданной функции в узлах интерполяции. Это позволяет записать систему из n линейного алгебраического уравнения относительно переменных a₁, a₂, a₃, ... a_nвида:

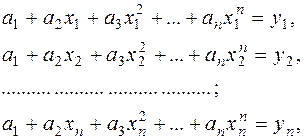
которая может быть разрешена любым из известных методов решения систем линейных алгебраических уравнений.

Использование такого подхода имеет и ряд недостатков. Во-первых, с увеличением количества узлов интерполяции n пропорционально возрастает и степень системы линейных алгебраических уравнений, а следовательно, к пропорциональному усложнению ее решения. Во-вторых с ростом n возрастает вероятность «биения» функции между узлами интерполяции за счет членов полинома с высшими степенями.

Ниже на рис.2 представлен фрагмент рабочей книги Excel с реализацией интерполяции многочленом

.

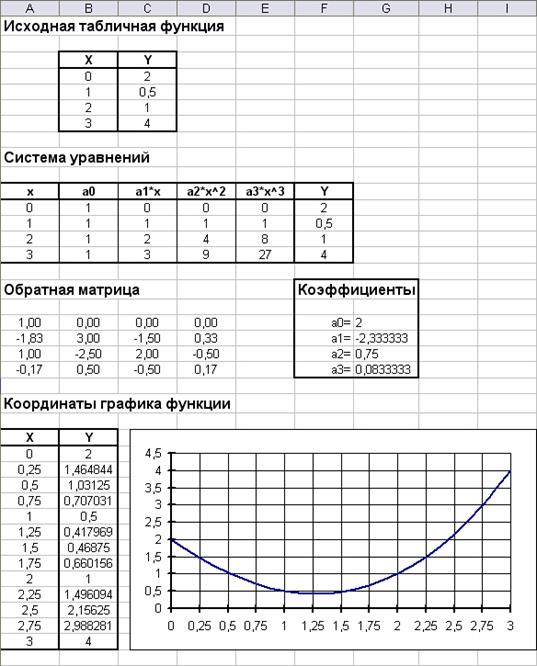Многочлен Лагранжа (J.L.Lagrange, 1795)

Представляет собой случай полиномиального представления приближающей функции, когда она ищется в виде линейной комбинации базисных функций j_k(x), которые должны быть определены для всего отрезка интерполяции [x₁, x_n], линейно независимы, и их количество должно быть равно числу узлов таблично заданной функции

.

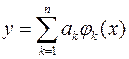Коэффициенты a₁, a₂, ..., a_n определяются исходя из условий равенства значений приближающей и исходной функций при табличных значениях аргумента, что сводит задачу к системе n линейных алгебраических уравнений относительно них, а в качестве функций j_k(x) используются полиномы (n–1) степени

,

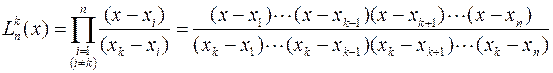которые для пяти узловых точек записываются в виде

,

,

,

,

.

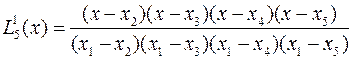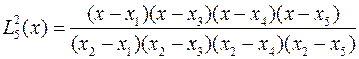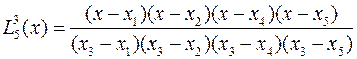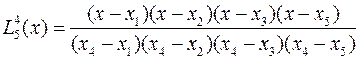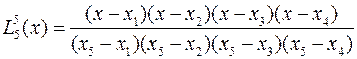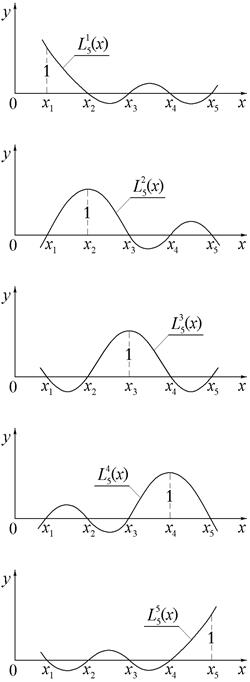
Для каждого полинома характерно то, что для всех значений x_i в узловых точках он принимает нулевые значения, кроме k-ой, где его значение равно единице.

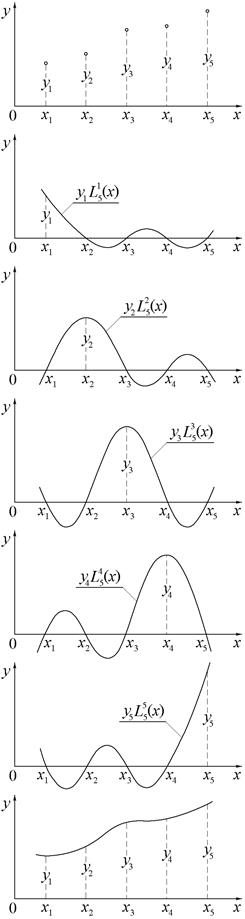
Графики этих полиномов пред­ставлены на рис.3.     При таком выборе базисных функций коэффициенты приближающей функции оказываются ординатами таблично заданной функции, а сама она приобретает харак-

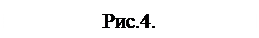
терный для многочлена Лагранжа вид:

.

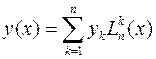Процесс построения интерполирующего многочлена Лагранжа для пяти узловых точек показан на рис.5.

Рассмотрим работу метода на приведенном выше примере. Сначала строятся четыре базовых полинома:

,

,

,

.

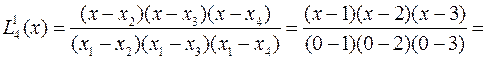
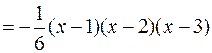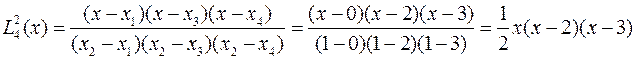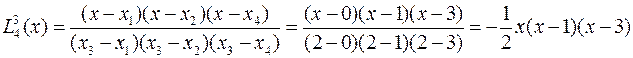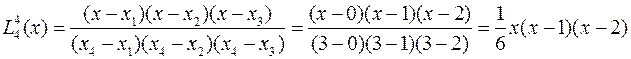Они позволяют записать интерполирующий многочлен Лагранжа в виде

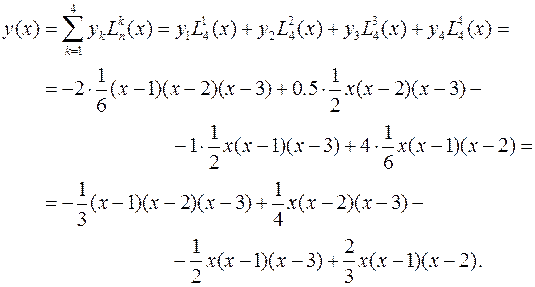
Для аргумента x = 1.6 многочлен Лагранжа даёт

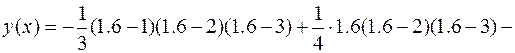
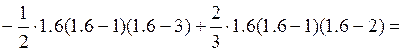
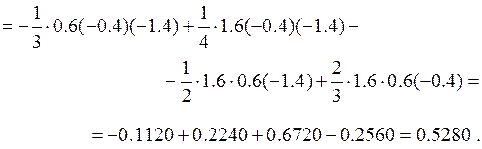
Ниже на рис.5 представлен фрагмент рабочей книги Excel с реализацией интерполяции с помощью многочлена Лагранжа.

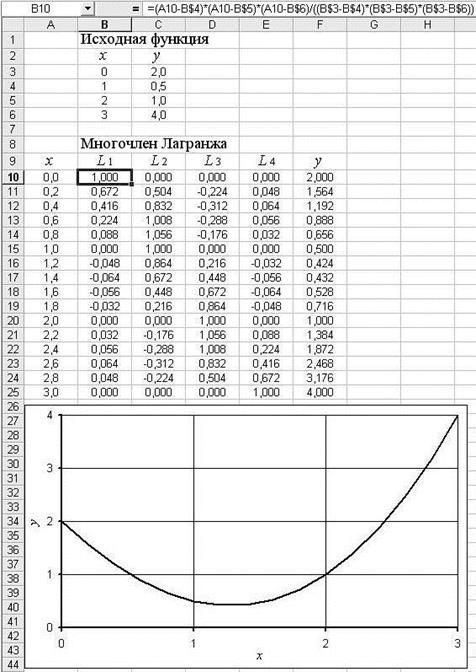
Рис.5.

Как видно из рисунка для аргумента x = 1.6 многочлен Лагранжа дал значение 0.528.

Для контроля правильности вычислений многочлена Лагранжа полезно строить графики базовых полиномов. Для рассматриваемого примера они приведены на рис.6.

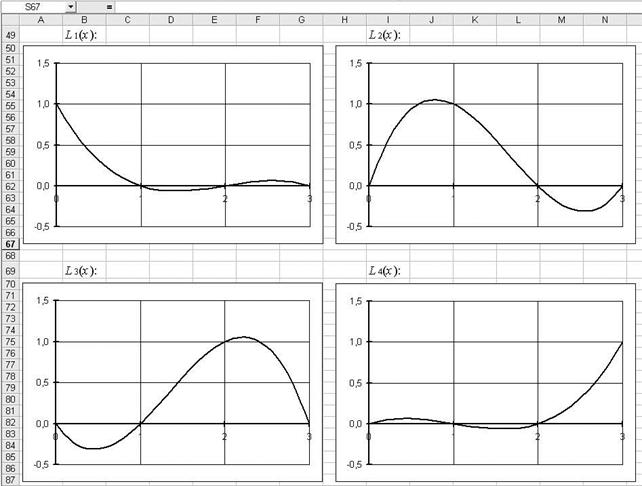
Рис.6.