Вывод закона Ньютона-Рихмана на основе закона Фурье.

Закон Ньютона — Рихмана — эмпирическая закономерность, выражающая тепловой поток между разными телами через температурный напор.

Теплоотдача — это теплообмен между теплоносителем и твёрдым телом.

Теплопередача — это теплообмен между двумя теплоносителями, разделённых твердым телом.

Закон утверждает:

Тепловой поток (выражается в Вт/м²) на границе тел пропорционален их разности температур (так называемый температурный напор):

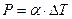(1.01)

Коэффициент теплоотдачи

Коэффициент пропорциональности α — коэффициент теплоотдачи (англ.), измеряется в Вт/(м²·К). В реальности он не всегда постоянен и может даже зависеть от разности температур, делая закон приблизительным. Если рассматривать тепловой поток как вектор, то он направлен перпендикулярно площадке поверхности, через которую протекает.

α — количество теплоты, отдаваемое с 1 м² поверхности за единицу времени при единичном температурном напоре. Он зависит:

от вида теплоносителя и его температуры;

от температуры напора, вида конвекции и режима течения;

от состояния поверхности и направления обтекания;

от геометрии тела.

Поэтому α — функция процесса теплоотдачи; величина расчётная, а не табличная; определяется экспериментально.

Эквивалентная запись:

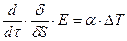(1.02)

Из вышеприведённой дифференциальной формулировки можно вывести интегральную:

Количество теплоты E, отданное через площадку на границе раздела тел площадью S за время τ , пропорционально разности температур этих тел (если считать, что она остаётся за это время постоянной):

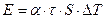(1.03)

Закон Ньютона служит одним из видов граничных условий (синоним — «условия третьего рода»), которые ставятся в задачах теплопроводности. В этом случае он записывается так (учтён также закон Фурье):

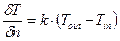
(1.04)

Заметим, что данный закон описывает ситуацию только на границе тела, внутри же температура определяется температуропроводностью тела. Тепловой поток внутри тела определяется по закону Фурье, что позволяет найти распределение, решив уравнение теплопроводности.

Если внутренняя теплопроводность намного больше, чем коэффициент теплоотдачи (иначе: маленькое число Био), то внутри устанавливается почти однородная температура (если на всей поверхности также она одинакова) и тогда можно записать уравнение охлаждения тела в виде:

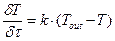(1.05)

Здесь коэффициент

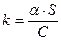(1.06)

где C — теплоёмкость тела.

T₀ - первоначальная температура остывающего тела.

T_out - температура окружающей среды.

T - температура тела через некоторое время, после того, как начался процесс остывания.

Из этого уравнения несложно получить, что температура тела в такой ситуации будет приближаться по экспоненте к температуре окружающей среды T_out.

Вывод закона Ньютона-Рихмана:

Выражение (1.05) это дифференциальное уравнение с разделёнными переменными.

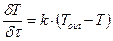(1.05)

Приводим к виду:

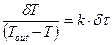(1.07)

Интегрируем:

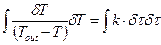(1.08)

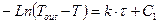(1.09)

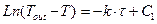(1.10)

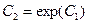(1.11)

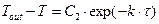(1.12)

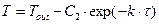(1.13)

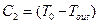(1.14)

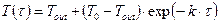(1.15)

k – величина, обратная постоянной времени τ _Θ , равной произведению теплового сопротивления на тепловую ёмкость:

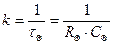(1.16)

k определяется выражением (1.06).

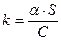(1.06)

где

C — теплоёмкость тела,

α — коэффициент теплоотдачи , измеряется в Вт/(м²·К).

Ватт Кельвин 1

Размерность k = ------------- ∙ ------------ = -----------

Кельвин Джоуль секунда

Параметр теплового сопротивления определяется следующим выражением (законом Фурье):

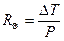(1.17)

Единица измерения теплового сопротивления:

1 Кельвин

1 тепловой Ом = ------------

1 Ватт

Размерность единицы теплового сопротивления:

1 Кельвин 1 Кельвин ∙ 1 секунду

1 тепловой Ом = ------------ = ------------------------------

1 Ватт 1 Джоуль

Параметр тепловой ёмкости определяется следующим выражением:

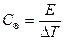(1.18)

Размерность единицы тепловой ёмкости:

1 Джоуль

1 тепловая фарада = ---------------

1 Кельвин

В тепловой цепи, при возникновении R_Θ C_Θ - цепочки, возникает параметр постоянной времени τ_Θ .

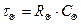(1.19)

Размерность постоянной времени τ_Θ - секунда.