Вторая интерполяционная формула Ньютона
Для интерполирования в конце таблицы обычно применяют вторую интерполяционную формулу Ньютона.
Пусть на [a,b] даны n + 1 различные значения аргумента х0, х1, …, хn ,, которым соответствуют следующие значения
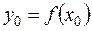 ;
; 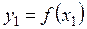 ; …;
; …; 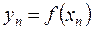 ,
,
а шаг интерполяции постоянен и равен h, т.е. 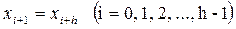 .
.
Построим интерполяционный многочлен вида
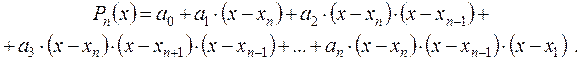
В этом многочлене неизвестны коэффициенты а0, а1, а2, …, аn . Их надо подобрать так, чтобы были возможны равенства:
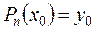 ;
; 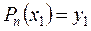 ; … ;
; … ; 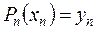 .
.
Для этого необходимо и достаточно, чтобы
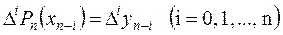 .
.
Коэффициент а0 найдем, положив х = хn в равенстве (7.4)
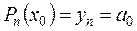
откуда
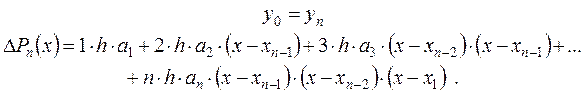
Отсюда, полагая х = хn-1 имеем 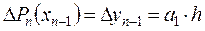 , следовательно
, следовательно
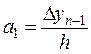 .
.
Из выражения для второй конечной разности имеем а2
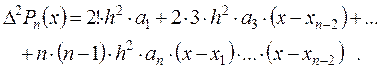
Полагая х = хn-2, получим
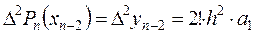 ,
,
откуда
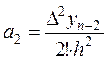 ,
,  .
.
Подставляя найденные значения коэффициентов, получим :
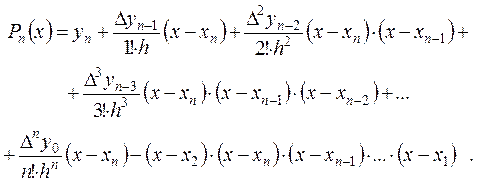
Это и есть вторая интерполяционная формула Ньютона. Положим q = (x - xn)/h, тогда
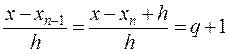 ;
; 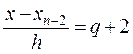 ;
;
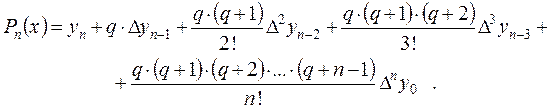 (7.5)
(7.5)
Первая интерполяционная формула Ньютона используется для интерполирования в начале отрезка [a,b], а вторая – на конечном участке таблицы.
Дата добавления: 2021-09-07; просмотров: 563;











