Вывод закона Ньютона-Рихмана на основе теории зарядов-энергий.

Определим температурные напоры для пределов интегрирования:

Начало процесса: ∆T₂ = T_out – T_Max

Результат процесса: ∆T₁ = T_out – T

T – температура тела в зависимости от прошедшего времени.(Температура тела в произвольный момент времени, прошедший от момента начала τ = 0)

T_out – температура окружающей среды.

Поток тепла остывающего тела на единицу температуры постоянен:

ΔP_Ед.Т=Const.

Отсюда следует:

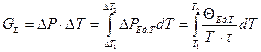(1.20)

Далее:

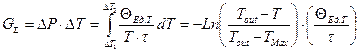(1.21)

Далее следует:

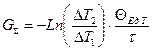(1.22)

Далее следует:

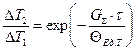(1.23)

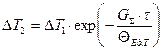(1.24)

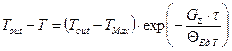(1.25)

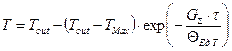(1.26)

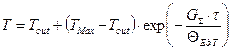(1.27)

Выражение (1.27) совпадает с (1.15)

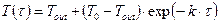(1.15)

Выводы:

1. G_Σ - суммарный флуктуационный ток остывающего тела равен константе.

2. Θ_Ед.T - удельная энергия 4-го уровня остывающего тела на единицу температуры равна константе.

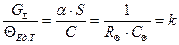(1.28)

G_Σ α ∙ S 1

----------- = -------------- = ----------- = k (1.28)

Θ_Ед.T. С R_Θ ∙ C_Θ

3. Аналогично, из теории зарядов-энергий, выводится закон для определения функциональной зависимости убывания тока в катушке, замкнутой на резистор при изменении времени.

4. Аналогично, из теории зарядов-энергий, выводится закон для определения функциональной зависимости убывания напряжения на обкладках конденсатора , замкнутого на резистор при изменении времени.

ПРИЛОЖЕНИЕ 3