Второй закон Ньютона

Количеством движения материальной точки называется векторная величина 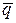, равная произведению массы точки на вектор ее скорости – .

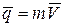Изменение количества движения пропорционально приложенной силе, направление вектора изменения количества движения совпадает с линией действия этой силы.

Математически этот закон записывается в виде векторного уравнения

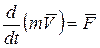, (1.1)

где m – масса движущейся точки; 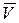– скорость движущейся точки; 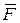– сила. Считая массу материальной точки величиной постоянной, второй закон Ньютона можно представить в виде формулы:

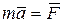, (1.2)

т.е. ускорение 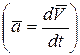, которое получает материальная точка, пропорционально действующей на точку силе. В таком виде в 1736г. основной закон записан Леонардом Эйлером (1707–1783).

Масса m входит в это уравнение, как коэффициент пропорциональности между силой и ускорением. Масса является характеристикой инертного свойства материальной точки, т.е. способности ее под действием заданной силы получать определенное ускорение. Если на точку действует одновременно несколько сил, то они, как известно, будут эквивалентны одной силе – равнодействующей 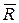, равной геометрической сумме этих сил. Тогда закон (1.2) примет вид

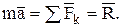(1.2а)

Этот же результат можно получить, используя вместо аксиомы параллелограмма аксиому независимого действия сил.

Аксиома. При одновременном действии на материальную точку нескольких сил ускорение точки, относительно инерциальной системы отсчета, от действия каждой отдельной силы, не зависит от наличия других приложенных к точке сил и равно векторной сумме ускорений от действия отдельных сил.

Второй закон (основной закон динамики) остается справедливым и для несвободной материальной точки, на которую наложены связи. Следует только в число приложенных внешних сил включить и силы реакций связей.