Оригиналы некоторых дробно-рациональных функций

При решении дифференциальных уравнений операторным методом, после того, как будет найдено изображение решения, иногда следует по изображению найти оригинал.

В общем случае эта задача решается с помощью преобразования, обратного преобразованию Лапласа-Карсона.

В более простых случаях, если изображение есть правильная рациональная дробь, то, разложив её на элементарные дроби, оригинал можно найти, используя полученную таблицу.

Известно, что элементарными дробями I рода называются дроби вида 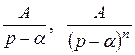, а элементарными дробями II рода называются дроби вида 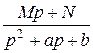и .

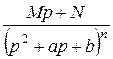Как найти для них оригиналы?

1. Для дроби 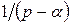оригинал найдем, используя правило интегрирования оригинала .

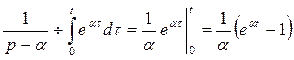2. Для получения оригинала функции 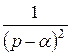воспользуемся изображением функции 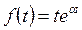и правилом интегрирования оригинала. Так как 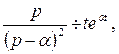то .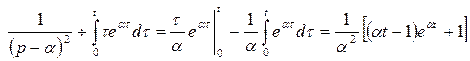

Аналогично можно найти оригиналы для функци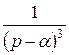й и .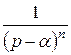

3. Как найти оригинал для функции ?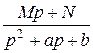

Корни знаменателя комплексные. Выделяя в знаменателе полный квадрат, можно его привести к виду 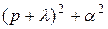или 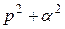. Оригинал дляфункции 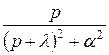можно найти, используя формулу 11 из таблицы 1, а для функции 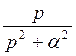- по формуле 6. Оригинал для функции 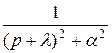можно найти, используя правило интегрирования оригинала. Так как

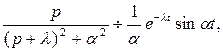то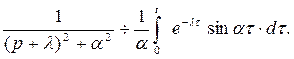

Вычислим определенный интеграл, используя формулу интегрирования по частям:

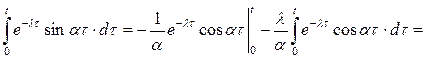
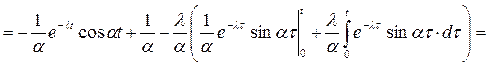
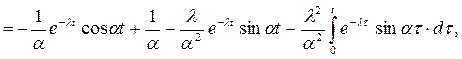тогда

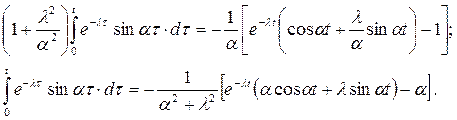
Таким образом: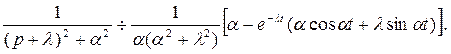

4. Найдём оригинал для элементарной дроби второго рода .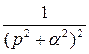

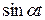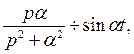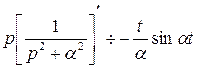Воспользуемся изображением и правилом дифференцирования изображения. Так как то , или

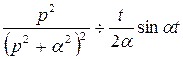.(2.4)

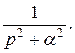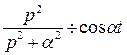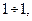Найдем оригинал для функции Так как и то 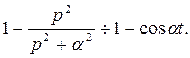Таким образом: 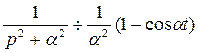.(2.5)

Из соотношений (2.4) и (2.5) и свойства линейности оператора Лапласа-Карсона получим:

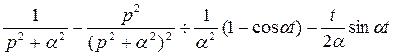, или

.

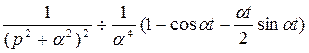Аналогичными преобразованиями можно получить оригиналы для других элементарных дробей II рода.