Операционный метод решения некоторых дифференциальных
Уравнений
Линейные дифференциальные уравнения с постоянными
Коэффициентами
Рассмотрим линейное неоднородное дифференциальное уравнение n-го порядка с постоянными коэффициентами.
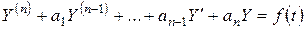 . (2.6)
. (2.6)
Найдем его частное решение 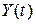 при
при 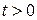 , удовлетворяющее начальным условиям:
, удовлетворяющее начальным условиям:
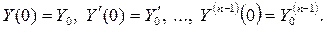 (2.7)
(2.7)
Применим к соотношению (2.6) оператор Лапласа-Карсона, т.е. умножим все члены равенства на 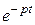 и проинтегрируем в пределах от 0 до
и проинтегрируем в пределах от 0 до 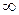 , затем результат умножим на p.
, затем результат умножим на p.
Обозначим 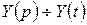 . Изображение производных найдем на основании правил дифференцирования и интегрирования оригинала. Изображение функции найдем по таблице 1 (см. с. 48). Таким образом, используя условия (2.7), получим:
. Изображение производных найдем на основании правил дифференцирования и интегрирования оригинала. Изображение функции найдем по таблице 1 (см. с. 48). Таким образом, используя условия (2.7), получим: 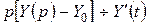 ;
; 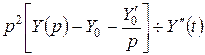 ;
;
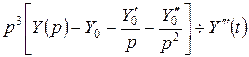 ; …;
; …; 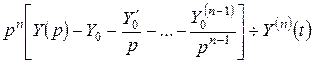 .
.
Запишем уравнение (2.6) в операторной форме.
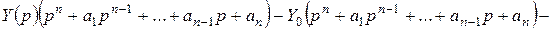
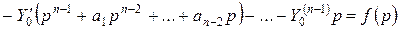 .
.
Обозначим через 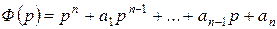 и
и
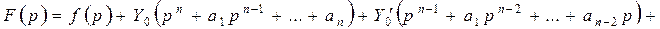
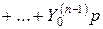 . Тогда
. Тогда 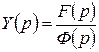 . Это есть изображение искомого частного решения. Оригинал находим или по таблице 1 или по формуле обращения, которая будет получена ниже.
. Это есть изображение искомого частного решения. Оригинал находим или по таблице 1 или по формуле обращения, которая будет получена ниже.
Если 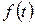 является линейной комбинацией функций вида
является линейной комбинацией функций вида 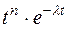 , то ее изображение есть рациональная дробь, показатель степени числителя которой не превышает показателя степени знаменателя. Такого же типа будет дробь
, то ее изображение есть рациональная дробь, показатель степени числителя которой не превышает показателя степени знаменателя. Такого же типа будет дробь 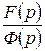 . Выделив целую часть и разложив оставшуюся элементарную дробь на простейшие, найдем оригинал
. Выделив целую часть и разложив оставшуюся элементарную дробь на простейшие, найдем оригинал 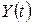 по таблице 1.
по таблице 1.
Решение дифференциального уравнения свелось к решению алгебраического уравнения, линейного относительно неизвестной функции 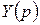 , и нахождению по изображению оригинала.
, и нахождению по изображению оригинала.
Пример 1. Постоянное напряжение, равное 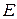 , включено в цепь с последовательно включенным постоянным сопротивлением
, включено в цепь с последовательно включенным постоянным сопротивлением 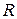 и самоиндукцией
и самоиндукцией 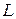 . Определить ток
. Определить ток 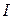 в цепи как функцию времени при
в цепи как функцию времени при 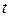 > 0, если
> 0, если 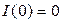 (см. рис. 2.1).
(см. рис. 2.1).

При последовательном соединении элементов падение напряжения в цепи складывается из падений напряжения на отдельных участках цепи. Поэтому
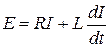 (2.8)
(2.8)
Обозначим 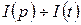 , тогда
, тогда 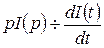 и
и 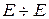 . В операторной форме дифференциальное уравнение (2.8) примет вид:
. В операторной форме дифференциальное уравнение (2.8) примет вид:
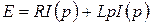 , тогда
, тогда 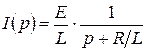 .
.
По формуле 3 таблицы 1 найдем 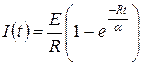 .
.
Пример 2
Дано 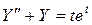 ;
; 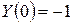 ;
; 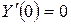 .
.
Найти 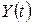 при
при 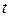 > 0. Пусть
> 0. Пусть 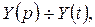 тогда
тогда 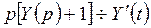 и
и 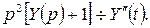 Применяя формулу 13 из таблицы 1, получим:
Применяя формулу 13 из таблицы 1, получим:
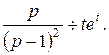
Запишем дифференциальное уравнение в операторной форме:
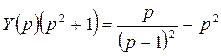 , или
, или 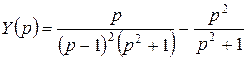 .
.
Разложив дробь на элементарные дроби, получим:
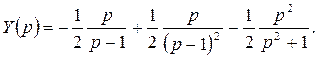 Тогда
Тогда 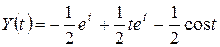 .
.
Пример 3
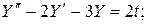
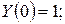
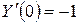 .
.
Найти 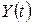 при
при 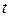 > 0. Пусть
> 0. Пусть 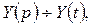 тогда
тогда
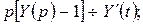
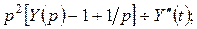
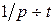 .
.
В операторной форме уравнение примет вид:
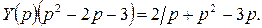 Отсюда
Отсюда
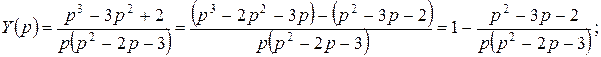
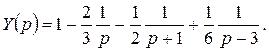 Тогда
Тогда
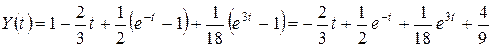 .
.
Дата добавления: 2020-07-18; просмотров: 839;











