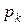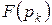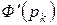Вывод формулы Хевисайда
Если изображение есть дробно-рациональная функция, удовлетворяющая некоторым условиям, то нахождение оригинала можно упростить, воспользовавшись формулой Хевисайда.
Пусть 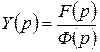 есть рациональная дробь.
есть рациональная дробь.
Формулу выведем при некоторых ограничениях:
1. Если показатель степени многочлена 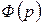 есть n, то показатель степени
есть n, то показатель степени 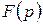 не больше n.
не больше n.
2. Все корни многочлена 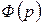 – простые.
– простые.
3. Среди корней многочлена 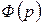 нет нуля.
нет нуля.
4. Числитель и знаменатель не имеют общих множителей, в противном случае их надо на этот множитель сократить (корни знаменателя не являются корнями числителя).
Замечание 1. Если 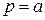 является корнем кратности k многочлена
является корнем кратности k многочлена 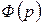 , то для многочлена
, то для многочлена 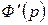
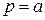 – корень кратности
– корень кратности 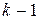 .
.
Пусть 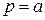 – корень кратности
– корень кратности 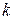 для многочлена
для многочлена 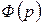 , тогда
, тогда 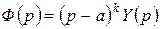 , где
, где 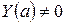 . Найдем производную от
. Найдем производную от 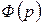 по переменной p:
по переменной p:
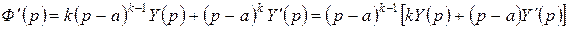 .
.
Выражение, стоящие в квадратных скобках, при 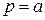 в нуль не обращается, потому для многочлена
в нуль не обращается, потому для многочлена 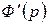
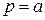 является корнем кратности
является корнем кратности 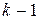 . Если
. Если 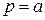 - простой корень многочлена
- простой корень многочлена 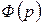 , то для
, то для 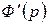
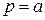 корнем не является.
корнем не является.
Вывод формулы Хевисайда.
Пусть 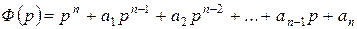 ; где
; где 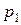 ,
, 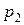 , …,
, …, 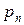 - корни
- корни 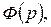 тогда
тогда 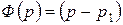 ···
··· 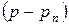 .
.
Показатель степени числителя дроби 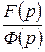 не превышает показателя степени знаменателя. Разделим
не превышает показателя степени знаменателя. Разделим 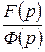 на p, чтобы гарантировать правильность дроби, и разложим получившуюся дробь на элементарные:
на p, чтобы гарантировать правильность дроби, и разложим получившуюся дробь на элементарные:
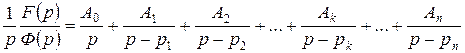 . (2.11)
. (2.11)
Определим коэффициенты 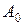 ,
, 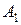 , …,
, …, 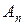 . Для этого умножим левую и правую части равенства (2.11) на p и, положив
. Для этого умножим левую и правую части равенства (2.11) на p и, положив 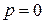 , найдем
, найдем 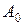 ;
; 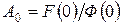 .
.
Умножив левую и правую части равенства (2.11) на 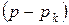 и положив
и положив 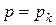 , найдем
, найдем 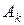 .
.
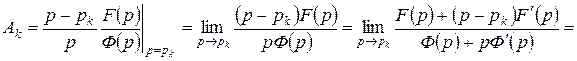
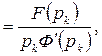 где
где 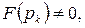
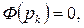
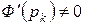 .
.
Тогда изображение есть 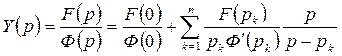 ,
,
соответственно, оригинал 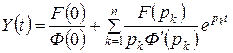 .
.
Пример 1. 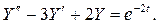 Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям: при
Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям: при 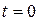
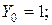
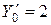 .
.
Запишем уравнение в операторной форме:
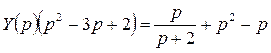 , или
, или 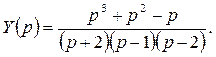
Применим формулу Хевисайда к функции 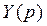 , где
, где 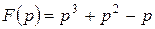 ,
,
|
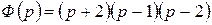 . Найдем
. Найдем 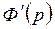 .
.
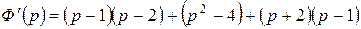 .
.
При этом 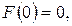
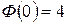 . Тогда оригинал
. Тогда оригинал
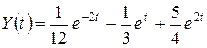 .
.
Замечание 2. Если корни знаменателя 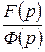 простые, но среди них есть нулевой корень, то оригинал можно получить, применяя к дроби
простые, но среди них есть нулевой корень, то оригинал можно получить, применяя к дроби 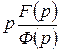 формулу Хевисайда и свойство об интегрировании оригинала.
формулу Хевисайда и свойство об интегрировании оригинала.
Пример 2. Найти частное решение дифференциального уравнения 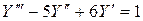 , удовлетворяющее начальным условиям: при
, удовлетворяющее начальным условиям: при 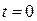
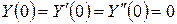 . Запишем уравнение в операторной форме:
. Запишем уравнение в операторной форме:
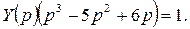 Отсюда
Отсюда 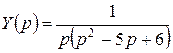 .
.
|
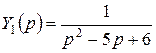 , где
, где
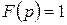 и
и 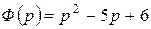 ,
, 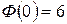 .
.
Найдем 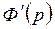 .
.
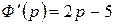 ,
, 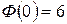 .
.
Тогда 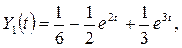 следовательно,
следовательно, 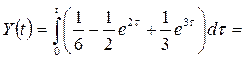
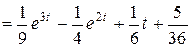 .
.
Замечание 3. В том случае, если среди корней 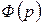 есть кратные, тоже можно составить формулу разложения. Но нахождение коэффициентов этой формулы сильно усложняется.
есть кратные, тоже можно составить формулу разложения. Но нахождение коэффициентов этой формулы сильно усложняется.
Рассмотрим пример на применение формулы Хевисайда, если многочлен 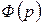 имеет мнимые корни.
имеет мнимые корни.
Пример 3. 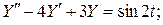
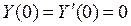 .
.
Запишем уравнение в операторной форме:
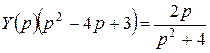 . Отсюда
. Отсюда 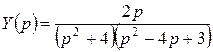 , где
, где 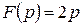 и
и 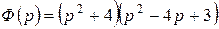 . При этом
. При этом 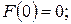
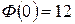 . Найдем
. Найдем 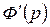 .
.
|
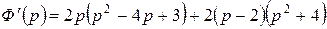 .
.
Тогда 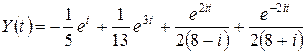 ,
,
или 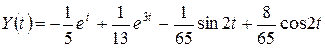 .
.
Дата добавления: 2020-07-18; просмотров: 917;