Интегродифференциальные уравнения
Рассмотрим задачу из электротехники.
Электрическая цепь состоит из последовательно включенных сопротивления 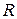 , емкости
, емкости 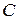 , индуктивности
, индуктивности 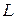 и ЭДС, меняющейся по некоторому закону
и ЭДС, меняющейся по некоторому закону 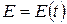 (см. рис. 2.2).
(см. рис. 2.2).
К моменту включения рубильника запас энергии в цепи равнялся нулю. Найти ток в цепи как функцию времени t. Элементы включены последовательно, поэтому падение напряжения в цепи складывается из падений напряжения на отдельных участках цепи.

Падение напряжения на сопротивлении есть 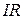 ; падение напряжения на емкости равно отношению количества электричества к емкости, т.е.
; падение напряжения на емкости равно отношению количества электричества к емкости, т.е. 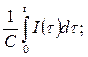 падение напряжения на индуктивности
падение напряжения на индуктивности 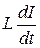 . Таким образом,
. Таким образом, 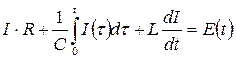 . Начальные условия
. Начальные условия 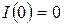 .
.
Решение задачи привелось к решению интегродифференциального уравнения вида: 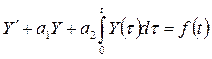 . Начальные условия:
. Начальные условия: 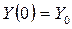 . Обозначим
. Обозначим 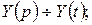
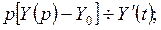
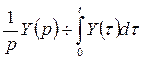 .
.
Запишем уравнение в операторной форме:
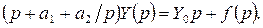 Найдем изображение
Найдем изображение 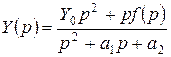 .
.
Оригинал находим по таблице или по формуле обращения. Аналогично может быть найдено решение уравнения, в которое входит неопределенный интеграл искомой функции, но в этом случае в начальных условиях нужно задать значение 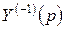 . Порядок интегродифференциального уравнения также может быть повышен.
. Порядок интегродифференциального уравнения также может быть повышен.
Пример 1. 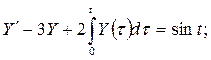
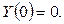
Данное уравнение в операторной форме имеет вид:
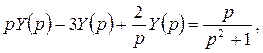 тогда
тогда 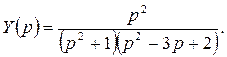
Разложив дробь на элементарные дроби
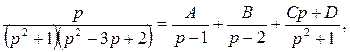 находим по методу неопределенных коэффициентов
находим по методу неопределенных коэффициентов 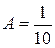 ;
; 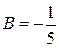 ;
; 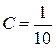 ;
; 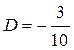 .
.
Тогда 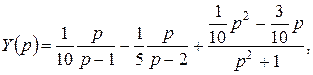 соответственно
соответственно
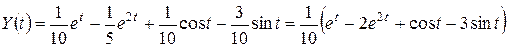 .
.
Дата добавления: 2020-07-18; просмотров: 647;











