Изображения основных элементарных функций
1. 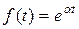 .Найдём
.Найдём 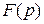 .
.
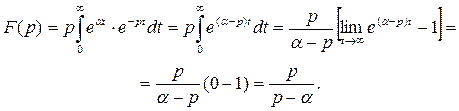
Таким образом, 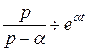 , при условии, что
, при условии, что 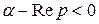 , или
, или 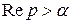 .
.
2. 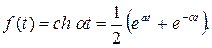 Найдём
Найдём 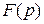 .
.
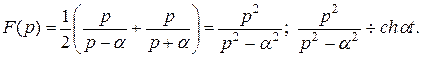
3. 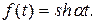 Найти
Найти 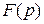 .
.
Изображение можно найти, выразив 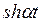 через показательную функцию или воспользовавшись свойством о дифференцировании оригинала. Так как
через показательную функцию или воспользовавшись свойством о дифференцировании оригинала. Так как 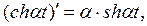 а
а 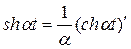 и
и 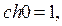 то
то
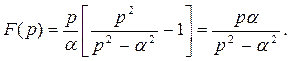 Таким образом,
Таким образом, 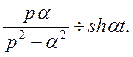
4. 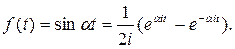 Найти
Найти 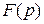 .
.
Воспользовавшись таблицей 1(см. конец гл.2), получим:
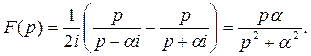 Таким образом,
Таким образом, 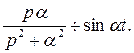
5. Найти
Найти 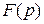 .
.
Воспользуемся свойством о дифференцировании оригинала:
Так как 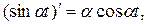 а
а 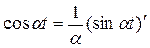 и
и 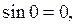 то
то
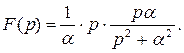 Таким образом,
Таким образом, 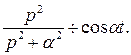
6. 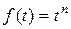 , n – целое число,
, n – целое число, 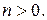 Найти F(p).
Найти F(p).
Воспользуемся соотношением 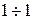 и свойством об интегрировании оригинала. Тогда имеем:
и свойством об интегрировании оригинала. Тогда имеем:
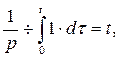 т.е.
т.е. 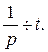
К полученному соотношению вновь применим свойство об интегрировании оригинала.
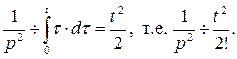
Проинтегрировав правую часть соотношения 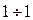 n раз, получим:
n раз, получим: 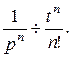 Следовательно,
Следовательно, 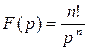 .
.
7. 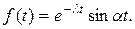 Найти
Найти 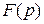 .
.
Воспользуемся теоремой смещения. Так как 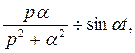 то
то
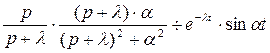 , или
, или 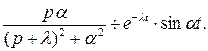
8. 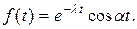 Найти
Найти 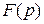 .
.
Так как 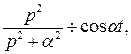 то по теореме смещения имеем
то по теореме смещения имеем
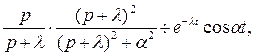 таким образом,
таким образом, 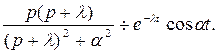
9. 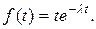 Найти
Найти 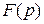 .
.
Можно воспользоваться теоремой смещения или свойством о дифференцировании изображения. Воспользуемся последним свойством:
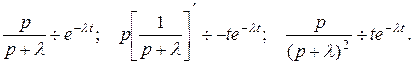
10. 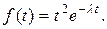 Найдём
Найдём 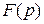 .
.
Применим ещё раз свойство о дифференцировании изображения к соотношению 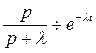 . Тогда имеем:
. Тогда имеем:
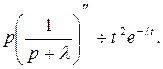 Так как
Так как 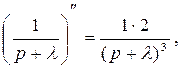 то
то 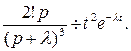
11. 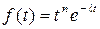 . Найти
. Найти 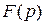 .
.
Дифференцируя n раз изображение, получим:
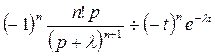 , или
, или 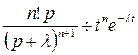 .
.
Дата добавления: 2020-07-18; просмотров: 644;











