Применение формулы Хевисайда к решению задач по электротехнике
К линейным дифференциальным уравнениям с постоянными коэффициентами или к системам таких уравнений приводится решение многих задач электротехники. Остановимся на рассмотрении некоторых из них.
Задача 1. Включение постоянной электродвижущей силы в контур, состоящий из индуктивности и емкости, шунтированной сопротивлением. Пусть постоянная ЭДС, индуктивность, емкость и сопротивление включены по приведенной схеме (см. рис. 2.3).

До замыкания рубильника зарядов в цепи не было, т.е. при 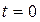
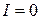 . Определить ток в катушке самоиндукции как функцию времени.
. Определить ток в катушке самоиндукции как функцию времени.
Падение напряжения в цепи складывается из падений напряжения на индуктивности и на участке цепи 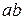 . Падение напряжения на участке
. Падение напряжения на участке 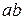 равно разности потенциалов на обкладках конденсатора. Обозначим его через
равно разности потенциалов на обкладках конденсатора. Обозначим его через 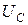 . Ток в катушке самоиндукции обозначим через
. Ток в катушке самоиндукции обозначим через 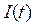 .
.
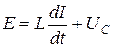 .
.
В этом уравнении две неизвестные – 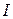 и
и 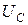 . Составим еще одно уравнение, используя закон Кирхгофа для случая параллельного включения элементов в цепь. Так как
. Составим еще одно уравнение, используя закон Кирхгофа для случая параллельного включения элементов в цепь. Так как 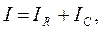
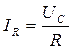 и
и 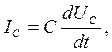 то
то 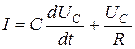 . В итоге получили систему уравнений:
. В итоге получили систему уравнений: 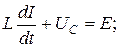
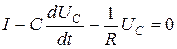 , относительно двух неизвестных
, относительно двух неизвестных 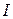 и
и 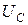 . Начальные условия:
. Начальные условия: 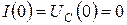 .
.
По условию задачи нужно найти только ток, так что решим эту систему относительно 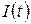 . Запишем систему в операторной форме. Пусть
. Запишем систему в операторной форме. Пусть 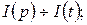
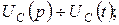
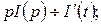
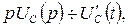 тогда
тогда 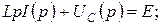
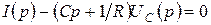 . Найдем
. Найдем 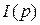 по формулам Крамера:
по формулам Крамера:
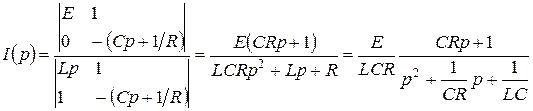 .
.
Корни уравнения 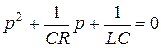 равны
равны 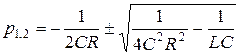 .
.
Обозначим 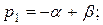
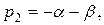 где
где 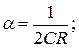
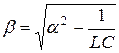 , тогда
, тогда
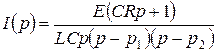 .
.
Найдем оригинал по формуле Хевисайда.
Если 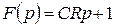 и
и 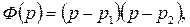
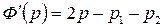 , при этом
, при этом 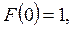
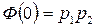 , то
, то
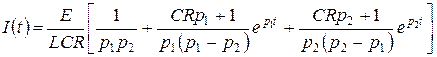 .
.
Произведем некоторые упрощения, пользуясь тем, что 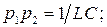
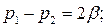
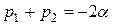 . Получим:
. Получим:
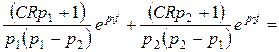
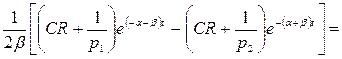
= 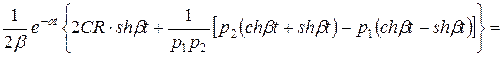
= 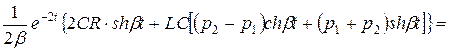
= 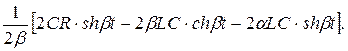
Итак, 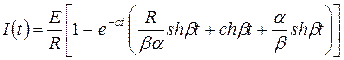 .
.
Если 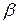 величина мнимая, то
величина мнимая, то 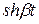 и
и 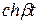 выражаются через тригонометрические функции по формулам
выражаются через тригонометрические функции по формулам 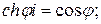
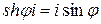 .
.
Задача 2. Включение постоянной электродвижущей силы в цепь, состоящую из двух индуктивно связанных контуров, не содержащих емкости.
В контур, состоящий из сопротивления 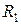 и индуктивности
и индуктивности 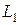 , включается постоянная ЭДС
, включается постоянная ЭДС 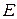 . Первый контур связан со вторым, состоящим из сопротивления
. Первый контур связан со вторым, состоящим из сопротивления 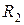 и индуктивности
и индуктивности 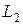 , взаимной индуктивностью M (см. рис. 2.4).
, взаимной индуктивностью M (см. рис. 2.4).
Включение производится при нулевых начальных условиях. Найти ток в первом контуре.
При включении рубильника электромагнитное поле первого контура индуцирует ток во втором контуре. Электромагнитное поле второго контура оказывает влияние на ток первого контура, коэффициент взаимной индукции M известен.
Составим дифференциальное уравнение для каждого контура:
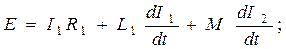
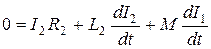 .
.
 Начальные условия: при
Начальные условия: при 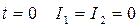 .
.
Рисунок 2.4
Если каждый контур содержит емкость, то в правых частях уравнений появятся слагаемые вида 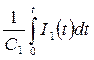 и
и 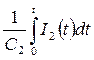 , что приведет к некоторому усложнению выкладок. Запишем уравнения в операторной форме.
, что приведет к некоторому усложнению выкладок. Запишем уравнения в операторной форме. 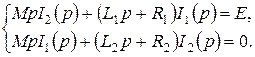
Найдем 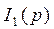 по формулам Крамера.
по формулам Крамера.
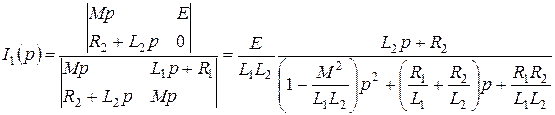 .
.
Введем обозначения: 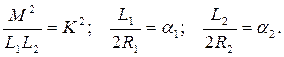
Найдем корни знаменателя 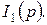
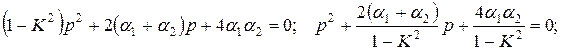
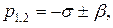 где
где 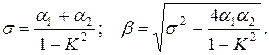
Тогда 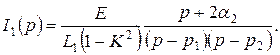
Найдем оригинал по формуле Хевисайда.
Если 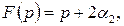
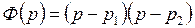 и
и 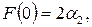
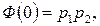 то
то 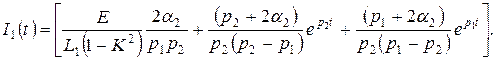
Выражение 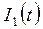 можно упростить и выразить через гиперболические функции, проделав преобразования. Подобные преобразования выполнены в прошлом примере.
можно упростить и выразить через гиперболические функции, проделав преобразования. Подобные преобразования выполнены в прошлом примере. 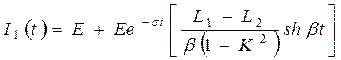 .
.
Дата добавления: 2020-07-18; просмотров: 746;











