Изменение масштаба (теорема подобия)
Пусть 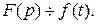 Как изменится изображение, если его аргумент умножится на число
Как изменится изображение, если его аргумент умножится на число 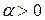 ? Обозначим
? Обозначим 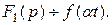 Тогда
Тогда
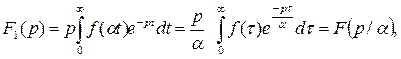
 где
где 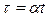 .
.
Итак, 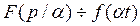 .
.
Если  является аналитическим выражением некоторого колебательного процесса, то теорема подобия позволяет найти изображение при изменении частоты оригинала.
является аналитическим выражением некоторого колебательного процесса, то теорема подобия позволяет найти изображение при изменении частоты оригинала.
Дифференцирование оригинала
Пусть 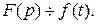 Каково изображение
Каково изображение 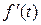 ?
?
Обозначим 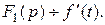 Тогда
Тогда
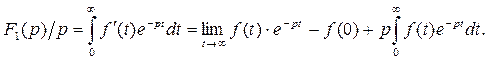
Если  – функция с ограниченным ростом, то
– функция с ограниченным ростом, то 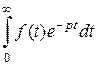 сходится при всех p,
сходится при всех p, 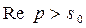 , где
, где 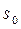 – показатель роста
– показатель роста  . Но это возможно, только если
. Но это возможно, только если 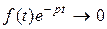 при
при 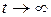 , а тогда
, а тогда 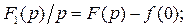
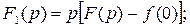
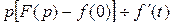 , где
, где 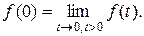
Если 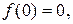 то
то 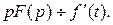 Следовательно, если функция удовлетворяет нулевому начальному условию, то при её дифференцировании изображение умножается на p.
Следовательно, если функция удовлетворяет нулевому начальному условию, то при её дифференцировании изображение умножается на p.
Пусть 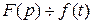 . Найдем изображение функции
. Найдем изображение функции 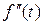 ,воспользовавшись свойством дифференцирования оригинала.
,воспользовавшись свойством дифференцирования оригинала.
Обозначим 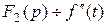 . Тогда
. Тогда
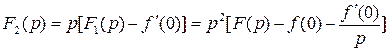 , или
, или 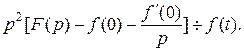
Если при 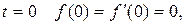 то
то 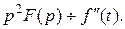
Аналогично можно найти изображение производной любого порядка.
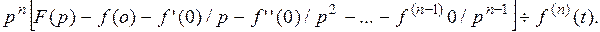
Если при 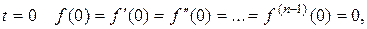 то
то 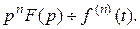
Следовательно, если функция  удовлетворяет нулевым начальным условиям, то при n–кратном её дифференцировании изображение умножается на
удовлетворяет нулевым начальным условиям, то при n–кратном её дифференцировании изображение умножается на 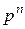 .
.
Дата добавления: 2020-07-18; просмотров: 818;











