РАСПРЕДЕЛЕНИЕ ФИШЕРА
Это распределение широко используется в дисперсионном анализе. Оно описывает случайную величину
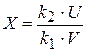 , (12)
, (12)
которая функционально связана с двумя случайными величинами U и V, имеющими 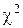 –распределения с k1 и k2 степенями свободы соответственно.
–распределения с k1 и k2 степенями свободы соответственно.
Плотность вероятности этого закона имеет вид
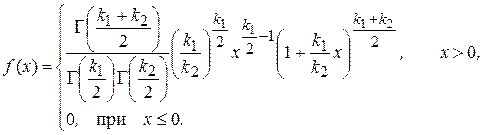
Математическое ожидание и дисперсия для этого закона равны
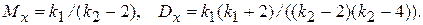
Для реализации случайной величины x, подчиненной распределению Фишера, необходимо, очевидно, сформировать две случайные величины U и V, подчиненные 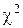 –распределению с k1 и k2 степенями свободы, и воспользоваться формулой (12). Тогда получим
–распределению с k1 и k2 степенями свободы, и воспользоваться формулой (12). Тогда получим
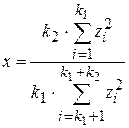 ,
,
где zi – значения нормально распределенной случайной величины с 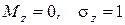 .
.
БЕТА–РАСПРЕДЕЛЕНИЕ
Плотность распределения вероятностей этого закона имеет вид
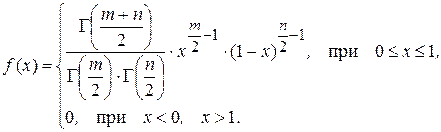 (13)
(13)
Математическое ожидание и дисперсия этого закона равны
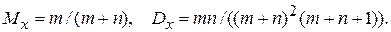
Для случайной величины, имеющей бета–распределение, можно записать:
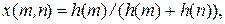
где 
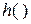 – случайная величина, имеющая хи–квадрат распределение.
– случайная величина, имеющая хи–квадрат распределение.
Так как
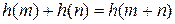 ,
,
то для реализации случайной величины x, подчиненной распределению (13), необходимо сформировать две случайные величины, имеющие 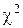 –распределение с m и m+n степенями свободы, а затем получить
–распределение с m и m+n степенями свободы, а затем получить
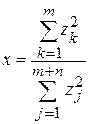 .
.
Дата добавления: 2016-06-22; просмотров: 2315;











