F-распределение Фишера

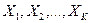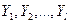Формальная модель – случайные величины и подчинены нормальному закону распределения с нулевым средним и произвольной дисперсией .

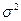Величины 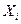не зависят от 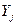. Кроме того, пусть среди 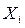имеется 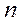, а среди 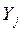– 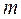линейно независимых величин.

Тогда случайная величина

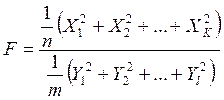
подчинена F-распределению с числами степеней свободы числителя 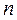и знаменателя .

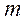Распределение Фишера находит применение при проверке оценок дисперсий, при статистической проверке вероятностных гипотез о качестве различных моделей случайных процессов.

Пример 5.1. Используя программу MS Excel, построим нормальный закон распределения на интервале (-3;3). Определим функцию распределения и функцию плотности распределения. Для этого воспользуемся стандартной функцией НОРМРАСП (значение; среднее; стандартное отклонение; интегральный). В нашем случае – нормированное нормальное распределение, поэтому среднее равно нулю, а стандартное отклонение - единице. Значит, в ячейке А19 запишем формулу =НОРМРАСП(А18; 0; 1; ИСТИНА), а в ячейке А20 - =НОРМРАСП(А18; 0; 1; ЛОЖЬ). В одной системе координат построим графики функций F(x) и f(x) (рис. 5.1 и 5.2).

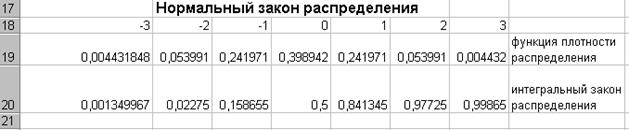
Рис. 5.1. Построение таблиц для нормального закона распределения

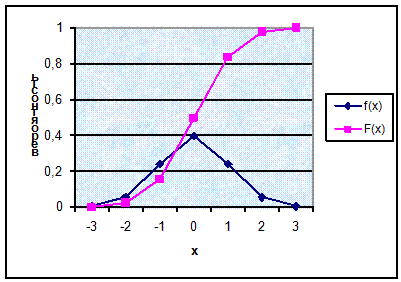
Рис. 5.2. Графики F(x) и f(x) для нормального закона распределения.