ОЦЕНКА КАЧЕСТВА ГЕНЕРИРУЕМОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ПО БЛИЗОСТИ ХАРАКТЕРИСТИК ЕЕ РАСПРЕДЕЛЕНИЯ К ТЕОРЕТИЧЕСКИМ ЗНАЧЕНИЯМ
Пусть теоретические значения математического ожидания и дисперсии случайной величины ξ, подчиняющейся некоторому закону распределения, равны Mξ,и Dξ.
Экспериментальные оценки этих характеристик получаются по формулам
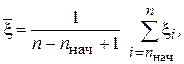
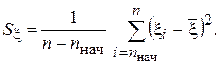
При вычислениях на ЭВМ дисперсию удобно вычислять по формуле
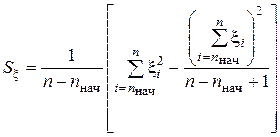 .
.
Близость оценки математического ожидания и его теоретического значения оценивается по критерию Стьюдента выражением
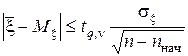 , (18)
, (18)
где 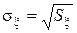 – оценка среднеквадратического отклонения случайной величины
– оценка среднеквадратического отклонения случайной величины 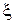 .
.
Если неравенство (18) не выполняется, то отклонение значимо и распределение нельзя считать соответствующим теоретическому.
Значение 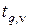 определяется по табл. 2 или табл. 3, но
определяется по табл. 2 или табл. 3, но 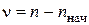 .
.
Близость дисперсий по критерию Фишера оценивается выражением
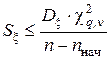 , (19)
, (19)
где 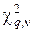 – коэффициент, определяемый по таблице
– коэффициент, определяемый по таблице 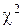 –распределения для q=0.01, 0.05, 0.1 и
–распределения для q=0.01, 0.05, 0.1 и 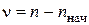 степеней свободы (см. табл. 4).
степеней свободы (см. табл. 4).
Таблица 4
Значения верхнего предела 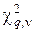 в функции q и ν
в функции q и ν
| ν | q | ν | q | ν | q | ||||||
| 0.10 | 0.05 | 0.01 | 0.10 | 0.05 | 0.01 | 0.10 | 0.05 | 0.01 | |||
| 2.7 | 3.8 | 6.6 | 17.3 | 19.7 | 24.7 | 29.6 | 32.7 | 38.9 | |||
| 4.6 | 6.0 | 9.2 | 18.5 | 21.0 | 26.2 | 30.8 | 33.9 | 40.3 | |||
| 6.3 | 7.8 | 11.3 | 19.8 | 22.4 | 27.7 | 32.0 | 35.2 | 41.6 | |||
| 7.8 | 9.5 | 13.3 | 21.1 | 23.7 | 29.1 | 33.2 | 36.4 | 43.0 | |||
| 9.2 | 11.1 | 15.1 | 22.3 | 25.0 | 30.6 | 34.4 | 37.7 | 44.3 | |||
| 10.6 | 12.6 | 16.8 | 23.5 | 26.3 | 32.0 | 35.6 | 38.9 | 45.6 | |||
| 12.0 | 14.1 | 18.5 | 24.8 | 27.6 | 33.4 | 36.7 | 40.1 | 47.0 | |||
| 13.4 | 15.5 | 20.1 | 26.0 | 28.9 | 34.8 | 37.9 | 41.3 | 48.3 | |||
| 14.7 | 16.9 | 21.7 | 27.2 | 30.1 | 36.2 | 39.1 | 42.6 | 49.6 | |||
| 16.0 | 18.3 | 23.2 | 28.4 | 31.4 | 37.6 | 40.3 | 43.8 | 50.9 |
При 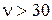
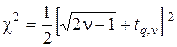 ,
,
где 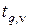 берется из табл. 3.
берется из табл. 3.
Если неравенство (19) не выполняется, то распределение нельзя считать соответствующим теоретическому.
Дата добавления: 2016-06-22; просмотров: 2014;











