I.1.7 СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ

1.Закон Максвелла о распределении молекул идеального газа по скоростям и энергиям

Важным является распределение числа молекул по скоростям. Движение молекул газа подчиняется законам статистической физики. В среднем скорости и энергии всех молекул одинаковы. Однако в каждый момент времени энергии и скорости отдельных молекул могут значительно отличаться от среднего значения.

Статистические методы позволяют найти функцию распределения молекул по скоростям, а также распределение числа молекул по кинетическим энергиям их беспорядочного теплового движения. Впервые это сделал К. Максвелл (1831 – 1879 г.г.), поэтому найденные им выражения называют функциями распределения Максвелла.

Приведём наиболее употребительную форму записи закона распределения молекул газа по скоростям (функцию распределения Максвелла)

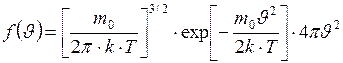, (I.28)

где 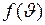= 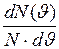– функция распределения, означающая относительное число молекул, скорости которых лежат в единичном интервале скоростей. Под знаком экспоненты в формуле (I.28) стоит отношение кинетической энергии молекулы (отвечающей данному значению скорости 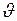) к величине 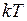, характеризующей среднее (по молекулам) значение этой энергии.

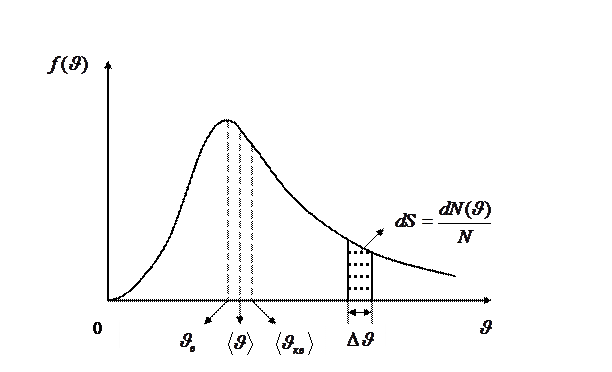
График функции (I.28) приведён на рис. 4. Вертикальными линиями отмечены три характерные скорости: наиболее вероятная 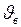, средняя 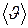и средняя квадратичная .

	Рисунок 4 – График функции распределения Максвелла

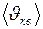При возрастании 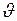множитель 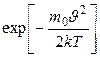уменьшается быстрее, чем растёт множитель 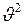и поэтому функция 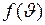, начинаясь от нуля, достигает максимума при 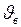и затем асимптотически стремится к нулю. Кривая несимметрична относительно .

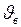Относительное число молекул 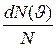, скорости которых лежат в интервале от 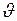до 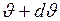, находится как площадь 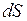заштрихованной полоски на рис.4. Площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Это означает, что функция 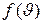удовлетворяет условию нормировки

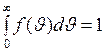. (I.29)

Наиболее вероятная скорость – скорость, при которой функция распределения молекул идеального газа по скоростям максимальна.Значение её определяется по формуле

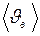
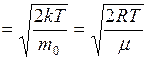. (I.30)

Из формулы (I.30) следует, что при повышении температуры максимум функции распределения молекул по скоростям (рис.5) сместится вправо (значение наиболее вероятной скорости становится больше).

Рисунок 5 - Графики функции распределения Максвелла, соответствующие различным значениям температуры

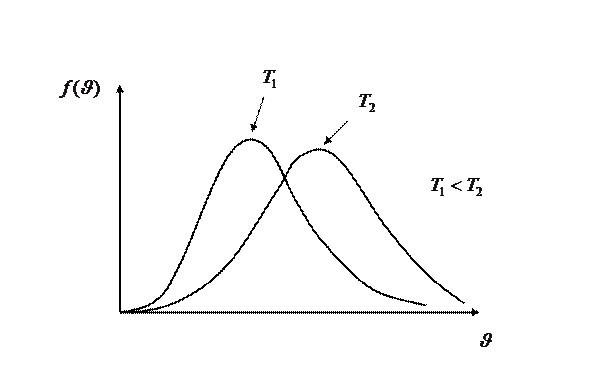
Площадь, ограниченная кривой, остаётся неизменной, в обоих случаях она равна единице. Поэтому при повышении температуры кривая распределения молекул по скоростям будет растягиваться и понижаться, что и видно на рис. 5.

Средняя скорость молекулы (средняя арифметическая скорость) определяется по формуле

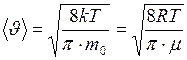. (I.31)

Согласно формулам (I.24), (I.30) и (I.31)

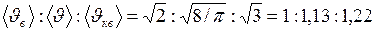. (I.32)

Таким образом, средняя и средняя квадратичная скорости превышают наиболее вероятную скорость на 13 и 22% соответственно.

От распределения по скоростям можно перейти к распределению молекул по значениям кинетической энергии поступательного движения. Эта энергия 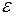связана со скоростью 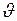соотношением

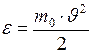. (I.33)

Распределение молекул по значениям кинетической энергии поступательного движения имеет вид

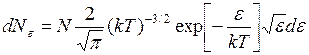, (I.34)

где 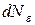- число молекул, кинетическая энергия поступательного движения которых заключена в пределах от 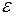до .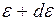

Из (I.34) следует, что функция распределения молекул по значениям 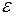имеет вид

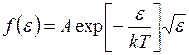, (I.35)

где 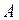– нормировочный множитель, равный .

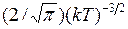2.Распределение частиц в потенциальном силовом поле (распределение Больцмана)

Если молекулы газа движутся в силовом поле (например, в поле тяготения Земли), то, преодолевая действие силы (за счет кинетической энергии), молекула приобретает в данном поле запас потенциальной энергии. Концентрация молекул ( 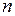), находящихся на высоте 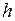от уровня отсчета и, следовательно, обладающих большим запасом потенциальной энергии, будет отличаться от концентрации молекул ( 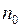), находящихся на нулевом уровне.

Для изотермической атмосферы распределение молекул по высоте будет иметь вид

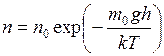. (I.36)

Из уравнения (I.36) следует, что с понижением температуры плотность молекул на высотах, отличных от нуля, убывает, обращаясь в нуль при 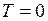. Это означает, что при абсолютном нуле все молекулы расположились бы на поверхности Земли. С повышением температуры зависимость концентрации от высоты становится всё более слабой, так что молекулы оказываются распределёнными по высоте почти равномерно. Такое поведение функции при изменении температуры объясняется тем, что она отражает «противоборство» двух тенденций:

– притяжение молекул к Земле (характеризуемое силой 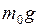) стремится расположить их на земной поверхности;

– тепловое движение (характеризуемое энергией 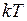) стремится разбросать молекулы равномерно по всем высотам.

При каждом конкретном распределении молекул по высоте (при каждом значении 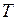) обе тенденции уравновешивают друг друга.

Выражение 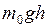представляет собой потенциальную энергию молекулы 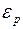. Поэтому формулу (I.36) можно записать следующим образом

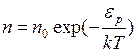, (I.37)

где 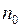– плотность молекул в том месте, для которого 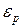принята равной нулю, 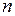– плотность молекул в том месте, где потенциальная энергия молекулы равна .

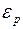Л. Больцман доказал, что формула (I.37) справедлива в случае потенциального силового поля любой природы для совокупности любых одинаковых частиц, находящихся в состоянии хаотического теплового движения. В связи с этим функцию (I.37) называют распределением Больцмана. Таким образом, распределение (I.36) представляет собой частный случай более общего распределения (I.37).

Так как концентрация газа 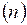пропорциональна его давлению, то формула связи концентраций молекул 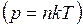, легко преобразуется в барометрическую, выражающую зависимость давления воздуха 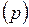от высоты 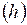при постоянной температуре

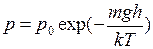, (I.38)

где 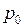– давление на высоте 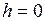; 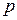– давление на высоте .

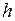Уравнение (I.38) называется барометрической формулой. Она позволяет найти атмосферное давление в зависимости от высоты или, измерив давление, найти высоту.

Прибор для определения высоты над земной поверхностью называется высотомером (или альтиметром). Его работа основана на использовании формулы (I.38). Из этой формулы следует, что давление с высотой убывает тем быстрее, чем тяжелее газ.