Барометрическая формула. Распределение Больцмана
Барометрическая формула – зависимость давления или плотности газа от высоты в поле силы тяжести.
Рассмотрим идеальный газ в равновесном состоянии внутри куба с ребром 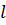 . Давление газа на рани куба обусловлено ударами молекул. Молекулы находятся в однородном поле тяготения, температура постоянна, масса всех молекул одинакова.
. Давление газа на рани куба обусловлено ударами молекул. Молекулы находятся в однородном поле тяготения, температура постоянна, масса всех молекул одинакова.
Действительно, молекулы любого газа в реальности находятся в поле тяготения Земли.
Тяготение и тепловое движение приводят газ в состояние, при котором его концентрация и давление убывают с высотой.
Если считать, что плотность газа по всему объёму постоянна  то аэростатическое давление на глубине
то аэростатическое давление на глубине  , будет равно:
, будет равно:
 , (1)
, (1)
где 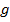 – ускорение свободного падения.
– ускорение свободного падения.
Формулой (1) можно пользоваться для вычисления давления очень тонких горизонтальных слоёв газа.
Пусть 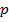 – давление газа на высоте
– давление газа на высоте  . Тогда с увеличением высоты на бесконечно малую величину
. Тогда с увеличением высоты на бесконечно малую величину 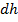 давление понизится на величину:
давление понизится на величину:
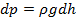 . (2)
. (2)
Из уравнения Менделеева –Клапейрона следует, что плотность газа равна:
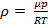 (3)
(3)
Тогда:
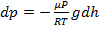 , (4)
, (4)
или
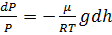 . (5)
. (5)
Проинтегрируем (5) от 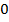 до
до  (при
(при 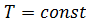 ):
):
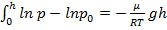 ,
,
где 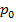 – давление на высоте
– давление на высоте 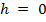 .
.
Тогда барометрическая формула примет вид:
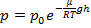 , (6)
, (6)
Из выражения (6) получим: 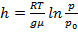 .
.
Давление газа связано с концентрацией молекул:
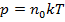 , (7)
, (7)
где 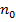 – число молекул в единице объёма (концентрация молекул).
– число молекул в единице объёма (концентрация молекул).
При 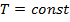 , получим:
, получим:
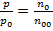 , (8)
, (8)
где 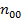 – концентрация молекул при давлении
– концентрация молекул при давлении 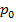 (при
(при 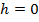 ).
).
Тогда уравнение (6) примет вид:  .
.
Так как 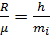 ,а
,а 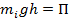 , где
, где 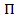 – потенциальная энергия молекулы в поле тяготения Земли.
– потенциальная энергия молекулы в поле тяготения Земли.
Получаем распределение Больцмана: 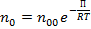
При постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул.
Если 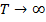 ,то
,то 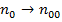 , т.е. повышение температуры ведёт к выравниванию концентрации молекул газа по объёму.
, т.е. повышение температуры ведёт к выравниванию концентрации молекул газа по объёму.
Если 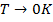 , то
, то 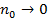 , т.е. все молекулы под действием силы тяжести будут опускаться на дно сосуда.
, т.е. все молекулы под действием силы тяжести будут опускаться на дно сосуда.
Атмосфера Земли существует лишь вследствие теплового движения частиц воздуха.
Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.
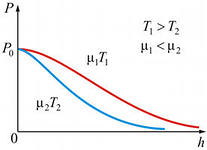 Рис. 115.
Рис. 115.
|
Барометрическая формула показывает, что плотность газа уменьшается с высотой по экспоненциальному закону. Чем выше температура
 , тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести
, тем медленнее убывает плотность с высотой. С другой стороны, возрастание силы тяжести 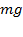 (при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести
(при неизменной температуре) приводит к значительно большему уплотнению нижних слоев и увеличению перепада (градиента) плотности. Действующая на частицы сила тяжести 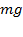 может изменяться за счёт двух величин: ускорения
может изменяться за счёт двух величин: ускорения 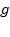 и массы частиц
и массы частиц 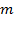 . Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте (рис. 115). На рис.115 показана зависимость концентрации различных газов от высоты. Видно, что число более тяжелых молекул с высотой убывает быстрее, чем легких.
. Следовательно, в смеси газов, находящейся в поле тяжести, молекулы различной массы по-разному распределяются по высоте (рис. 115). На рис.115 показана зависимость концентрации различных газов от высоты. Видно, что число более тяжелых молекул с высотой убывает быстрее, чем легких.
Реальное распределение давления и плотности воздуха в земной атмосфере не следует барометрической формуле, так как в пределах атмосферы температура и ускорение свободного падения меняются с высотой и географической широтой. Кроме того, атмосферное давление увеличивается с концентрацией в атмосфере паров воды.
Дата добавления: 2016-09-26; просмотров: 5674;











