НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Воспользуемся центральной предельной теоремой Ляпунова из теории вероятностей. В простейшей форме сущность этой теоремы состоит в том, что
закон распределения суммы m независимых случайных величин, имеющих один и тот же произвольный закон распределения, при неограниченном увеличении числа слагаемых m приближается к нормальному.
В случае равномерно распределенных в интервале (a, b) независимых случайных чисел сумма m таких чисел стремится к нормальному распределению с математическим ожиданием
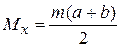
и дисперсией
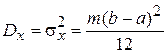 .
.
Если а=0 и b=1, то
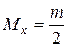 ;
; 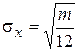 .
.
Для получения последовательности нормально распределенных случайных чисел с заданными параметрами Mx, 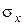 представим случайную величину х в виде суммы
представим случайную величину х в виде суммы
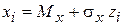 , (6)
, (6)
где zi – нормально распределенная случайная величина с параметрами Mz=0, 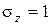 .
.
Рассмотрим, как получить случайную величину zi, располагая последовательностью равномерно распределенных в интервале (0, 1) случайных чисел 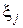 . Согласно центральной предельной теореме имеем
. Согласно центральной предельной теореме имеем
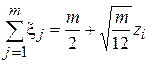 .
.
Отсюда
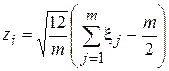 .
.
Подставив значение zi в (6), получим
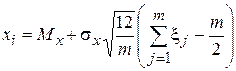 .
.
Принимая m=12, находим

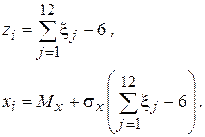
Дата добавления: 2016-06-22; просмотров: 1941;











