МОДЕЛИРОВАНИЕ ДИСКРЕТНЫХ РАСПРЕДЕЛЕНИЙ

Дискретные распределения случайных величин применяют для описания поведения случайных событий.

Алгоритм моделирования на ЭВМ случайных событий с известным законом распределения вероятностей сводится к следующему.

Пусть заданы значения вероятностей P₁, P₂,…, P_n для независимых событий A₁, A₂,…, A_n, образующих полную группу. Нужно определить в каждом испытании, какое из этих событий произошло.

Разобьем отрезок [0,1] на n отрезков так, чтобы длина i–го отрезка равнялась вероятности P_i. Выберем из равномерного в интервале (0,1) распределения случайное число 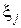и определим, на какой участок попадает это число. Попадание случайного числа 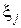на k–й участок фиксируем как факт свершения события A_k . На ЭВМ этот процесс сводится к выбору случайного числа 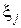и проверке условия

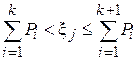. (15)

Для фиксированного 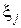неравенство выполняется лишь при одном значении k. Это значение k и определяет номер события A_k , которое произошло в данном опыте. Cвершение события A_k означает, что случайная величина x приняла значение k.

В рассматриваемых ниже законах суммы вероятностей монотонно возрастают с ростом i, поэтому вместо неравенства (15) можно использовать одностороннюю границу вида

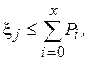(16)

а поиск значения x производить последовательным вычитанием P_i из 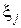до первого результата, не превышающего 0. Значение i, при котором это произойдет, и принимается за значение случайной величины x.

Вычисления реализуются достаточно просто, так как для рассматриваемых законов очередное значение вероятности P_i+1 определяется по рекуррентной формуле вида

P_i+1 = P_i r(i) ,

где r(i) – определяется законом распределения случайной величины.