БЕСПОВТОРНЫЕ СЛУЧАЙНЫЕ ЧИСЛА
В случае, когда необходимы бесповторные случайные числа, можно воспользоваться принципами создания автономной линейной последовательностной машины (АЛПМ) или покоящейся линейной последовательностной машины (ПЛПМ), которые способны генерировать 2n–1 различных двоичных чисел, где n – разрядность машины.
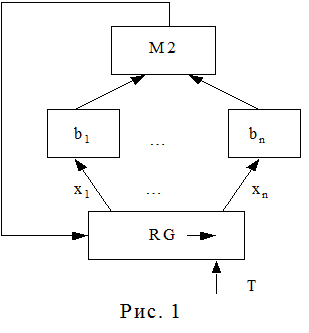 |
АЛПМ (рис. 1) представляет собой регистр сдвига с обратной связью, формируемой элементом М2. Элементы bi фиктивны – они имитируют наличие связи выхода i–го разряда регистра с элементом М2 (bi = 1) или ее отсутствие (bi = 0). Максимальный период 2n–1 повторения чисел получается только при определенных значениях bi, которые образуются из коэффициентов многочленов максимального показателя
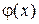 , приведенным в [4 (табл. 5)].
, приведенным в [4 (табл. 5)].
Правило их определения сводится к следующему.
Если представить 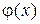 в виде
в виде
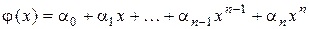 ,
,
где 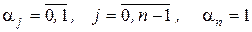 , то bi можно найти из выражения
, то bi можно найти из выражения
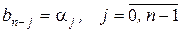
Таким образом получаем
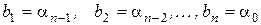 .
.
Индексы коэффициентов bi, равных 1 и позволяющих построить АЛПМ максимального периода, для некоторых n даны в табл. 1.
Таблица 1
Индексы единичных коэффициентов bi,
порождающих АЛПМ максимального периода 2n–1
| n | Индексы | n | Индексы |
| 1, 2 | 9, 11 | ||
| 1, 3 или 2, 3 | 6, 8, 11, 12 | ||
| 1, 4 или 3, 4 | 9, 10, 12, 13 | ||
| 3, 5 | 9, 11, 13, 14 | ||
| 5, 6 | 14, 15 | ||
| 6, 7 | 11, 13, 14, 16 | ||
| 4, 5, 6, 8 | 10, 30, 31, 32 | ||
| 5, 9 | 60, 61, 63, 64 | ||
| 7, 10 | 92. 93, 98, 100 |
В [4 (табл. 5)] даны коэффициенты полиномов максимального показателя для 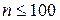 , 107, 127.
, 107, 127.
АЛПМ максимального периода генерирует псевдослучайные целые числа от 1 до 2n–1, причем первое число определяется ее начальным состоянием X0 (состоянием разрядов ее регистра сдвига в начальный момент времени).
ПЛПМ максимального периода получается из АЛПМ добавлением одного входа схемы М2, на который подается логическая единица. Такая ПЛПМ способна генерировать целые числа от 0 до 2n–2.
Поскольку все числа различны, то мы имеем равномерное распределение на интервале (1, 2n – 1) или (0, 2n-2). Если рассматривать числа на интервале меньше предельного, то равномерность может нарушиться. Практика показывает, что это нарушение незначительно.
Для получения чисел в интервале (0,1) достаточно разделить числа, получаемые АЛПМ или ПЛПМ, на период 2n–1. При этом для АЛПМ получим числа в интервале 
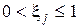 , а для ПЛПМ в интервале
, а для ПЛПМ в интервале 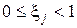 .
.
Если необходимы и 0, и 1, то для АЛПМ надо искусственно получить 0 либо в начале последовательности, либо в ее конце, а для ПЛПМ так надо поступить с 1.
Смоделировать работу АЛПМ или ПЛПМ программным способом можно двояко: либо на битовом уровне, производя сдвиг слова (слов) и выделяя его (их) разряды для формирования обратной связи, либо представив регистр в виде одномерного массива, элементы которого соответствуют его разрядам, и производя все необходимые действия с элементами этого массива.
Дата добавления: 2016-06-22; просмотров: 1914;











