ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Численное интегрирование (историческое название: (численная квадратура)) – это вычисление определенных интегралов от функций, заданных либо в явном виде (например, 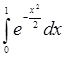), либо в виде таблицы. К численному интегрированию прибегают тогда, когда точными методами интеграл вычислить либо невозможно, либо сложно. Например, аналитическое представление подынтегральной функции известно 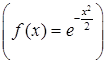, но её первообразная не выражается через аналитические функции. Если подынтегральная функция задана аналитически, то ее приводят к табличному виду, задавая шаг h и вычисляя значения функции в определенных точках. Интегралы вычисляют с помощью так называемых квадратурных формул, то есть

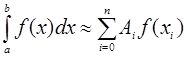(5.1)

Для нахождения коэффициентов 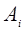в формуле (5.1) функцию 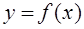на каждом из отрезков [x_i, x_i+1] заменяют интерполяционным полиномом. Интеграл от полинома легко вычисляется. Для нахождения двойных определенных интегралов существуют соответствующие кубатурные формулы (с двойными суммами).

Квадратурные формулы прямоугольников, трапеций, Симпсона для вычисления определенных интегралов