Решение задачи численного интегрирования в Scilab

При вычислении определенных интегралов от функций, заданных в виде таблицы или в явном виде ( 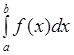), одним из численных методов используют функции intsplin, inttrap, integrate, intg.

Вычислим интеграл из примера 5.1 с помощью команды intsplin. Это интегрирование экспериментальных данных с помощью сплайн-интерполяции. Известно значение интегрируемой функции в дискретных точках (узлах).

-->x=1:.4:5;

-->y=(x.*log(x)+sin(x))./(cos(x)+2);

-->v=intsplin(x,y)

Получаем:

v = 10.186009

Или:

-->x=[1 1.4 1.8 2.2 2.6 3 3.4 3.8 4.2 4.6 5];

-->y=[0.3312484 0.6712133 1.1461338 1.8017036 2.6242688 3.4029023 3.7797992 3.6898487 3.4150132 3.1920841 3.1039027];

-->v=intsplin(x,y)

v = 10.186009

Тот же интеграл вычислим с помощью функции inttrap. Интегрирование экспериментальных данных производится по формуле трапеций. Задав те же самые x и y, получаем:

v=inttrap(x,y)

v = 10.176217

Остальные функции используют, когда подынтегральная функция задана явно.

Функция integrate. Это интегрирование по квадратуре. Может задаваться требуемая точность вычислений.

Синтаксис функции: [x]=integrate(f,v,a,b [,atol [,rtol]])

Параметры функции:

f –подынтегральная функция;

v – переменная интегрирования;

a, b – пределы интегрирования;

atol, rtol – действительные числа, абсолютная и относительная ошибки соответственно. Первая по умолчанию равна 10^-8, вторая 10^-14.

Ниже показано, как можно вычислить интеграл с помощью данной функции.

--> integrate('(x*log(x)+sin(x))/(cos(x)+2)','x',1,5)

ans = 10.186238

Можно это сделать и так:

clc

function y=f(x), y=(x.*log(x)+sin(x))./(cos(x)+2);endfunction

t=integrate('f','x',1,5);printf("Интеграл равен %2.6f",t);disp("")

Получаем:

Интеграл равен 10.186238

Функция intg имеет такой синтаксис:

[v, err [,ierr]]=intg(a, b, f [,ea [,er]])

Параметры функции:

a, b – пределы интегрирования;

ea, er – действительные числа, абсолютная и относительная ошибки соответственно. По умолчанию равны 10^-13 и 10^-8.

err – оценка абсолютной ошибки результата.

Вот код с использованием этой функции для вычисления интеграла из примера 5.1.

clc

function y=f(x), y=(x.*log(x)+sin(x))./(cos(x)+2);endfunction

t=intg(1,5,f);printf("Интеграл равен %2.6f",t);disp("")

Результат:

Интеграл равен 10.186238

ЛИТЕРАТУРА

1. Шарый, С.П. Курс вычислительных методов / С.П. Шарый. – Институт вычислительных технологий СО РАН, Новосибирский государственный университет, 2020. – 639 с.

2. Самарский, А.А. Численные методы / А.А. Самарский, А.В. Гулин. – М.: Наука, 1989. – 432 с.

3. Демидович, Б.П. Основы вычислительной математики / Б.П. Демидович, И.А. Марон. – М.: Наука, 1970. – 664 с.

4. Мудров, В. И. Метод наименьших модулей / В. И. Мудров, В. Л. Кушко. – М.: Знание, 1971. – 64 с.

5. Брановицкая, С.В. Вычислительная математика в химии и химической технологии / С.В. Брановицкая. – Киев, Издательское объединение «Вища школа», 1986. – 216 с.

6. Scilab: Решение инженерных и математических задач / Е.Р. Алексеев [и др.]. – М.: БИНОМ, 2008. – 260 с.

7. Решение инженерных задач в Scilab: учебное пособие / А.Б. Андриевский [и др.]. – СПб.: НИУ ИТМО, 2013. – 97 с.

8. Ерин, С.В. Scilab – примеры и задачи: учебное пособие / С.В. Ерин. – М.: Лаборатория «Знания будущего», 2017. – 154 с.

9. Michael Baudin. Введение в Scilab. Перевод Artem Glebov, 2010. – 85 с. [Электронный ресурс]. Свободный.

10. Кобзарь, А.И. Прикладная математическая статистика: для инженеров и научных работников / А.И. Кобзарь. – М.: Физматлит, 2006. – 816 с.

11. Орлов, А.И. Прикладная статистика / А.И. Орлов. – М.: Экзамен, 2004. – 656 с.

12. Титов, А.Н. Решение задач теории вероятностей и математической статистики в среде Scilab: учебно-методическое пособие / А.Н. Титов, Р.Ф. Тазиева. – Казань: Изд-во КНИТУ, 2019. – 120 с.

13. Лутманов, С. В. Курс лекций по методам оптимизации. – Ижевск: НИЦ РХД, 2001. – 368 с.

14. Гольдштейн, А. Л. Оптимизация в среде Matlab: учеб. пособие / А. Л. Гольдштейн. – Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2015. – 192 с.

15. Крутова, В.И. Основы научных исследований: учебник для вузов / В.И. Крутова, В.В. Попова. – М.: Высшая школа, 1989. – 400 с.

16. Титов, А.Н. Решение задач линейной алгебры и прикладной математики в среде Scilab: учебно-методическое пособие / А.Н. Титов, Р.Ф. Тазиева. – Казан. нац. исслед. технол. ун-т. – Казань: Изд-во КНИТУ, 2020. – 98 с.