Численное дифференцирование с помощью интерполяционных полиномов
Если шаг в таблице постоянный, то на первом этапе строят интерполяционный полином Ньютона.
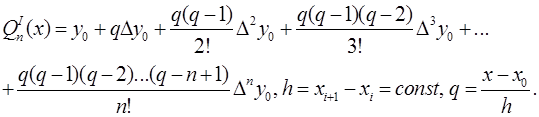
Найдем первую производную от этого полинома. 
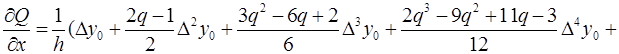
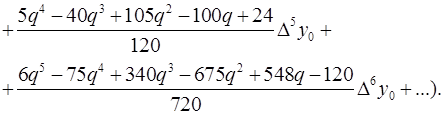 (4.1)
(4.1)
Аналогично,
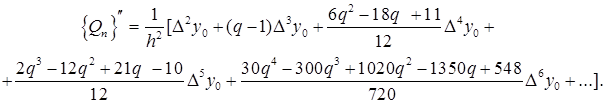 (4.2)
(4.2)
Если производную нужно вычислить в каком-либо узле таблицы (например, в точке х=х0), то формулы (4.1) и (4.2) упрощаются, так как 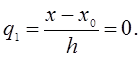
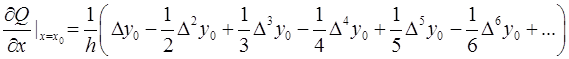 (4.3)
(4.3)
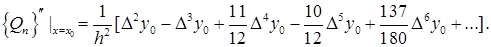 (4.4)
(4.4)
Пример 4.1. Зависимость вязкости (η) нитробензола от температуры выражается следующими экспериментальными данными [5]:
| Т, К | 283,15 | 293,15 | 303,15 | 313,15 | 323,15 | 333,15 | 343,15 |
| η, мПа·с | 2,509 | 2,013 | 1,682 | 1,438 | 1,251 | 1,094 | 0,970 |
Найти абсолютный температурный коэффициент вязкости 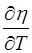
а) при Т=288,15 К; b) при температуре Т=283,15 К.
Решение. Так как шаг в приведенной выше таблице – постоянный, для решения задачи воспользуемся формулой (4.1). Составим таблицу конечных разностей: 
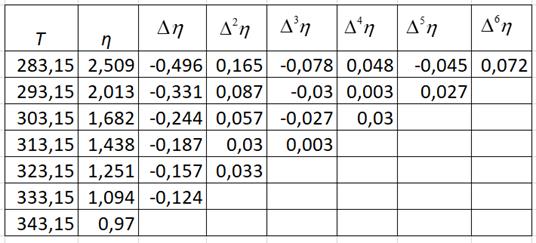
Имеем:
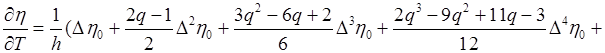
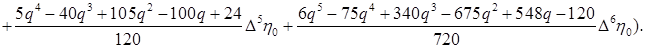
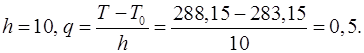
Подставляя в приведенную формулу данные из таблицы, получаем:
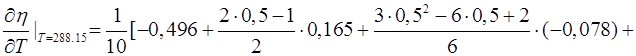
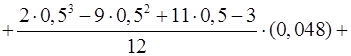
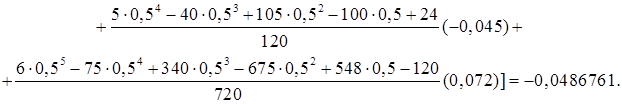 Найдем теперь значение производной в узле таблицы – при Т=283,15.
Найдем теперь значение производной в узле таблицы – при Т=283,15.
В этом случае 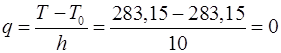 и можно воспользоваться формулой (4.3).
и можно воспользоваться формулой (4.3).
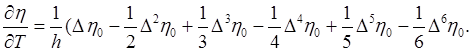
Имеем:
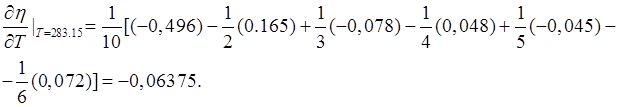
Данный пример приведен исключительно в иллюстративных целях, чтобы показать, как работают формулы численного дифференцирования. При решении реальной задачи, связанной с вычислением производных, лучше, на наш взгляд, получить уравнение интерполяционного полинома, как это сделано в разделе 3, а затем вычислить от него производную/ые. Можно воспользоваться также программой, приведенной на с. 66.
Для вычисления значений производных в узлах таблицы в зависимости от количества узлов и расположения точки, в которой нужно вычислить производную, существуют формулы численного дифференцирования, не такие громоздкие, как формулы (4.1) и (4.2). Приведем некоторые из них (см. табл. 4.1). Шаг в таблице должен быть постоянным.
Отметим, что численное дифференцирование относится к числу некорректных задач. Это означает, что небольшие погрешности в исходных данных могут привести к большим погрешностям в результате решения задачи. По этой же причине следует крайне осторожно пользоваться формулами численного дифференцирования при вычислении производных старших порядков.
Таблица 4.1
Формулы численного дифференцирования
Формула
| Оценка погрешности |
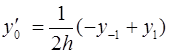
| 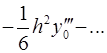 
|
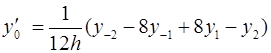
| 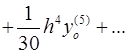
|
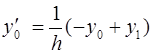
| 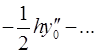
|
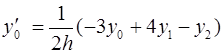
| 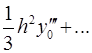
|
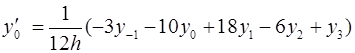
| 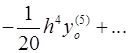
|
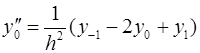
| 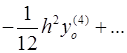
|
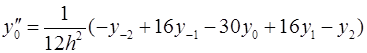
| 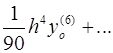
|
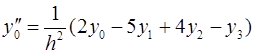
| 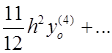
|
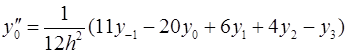
| 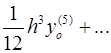
|
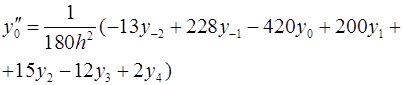
| 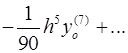
|
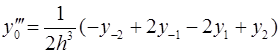
| 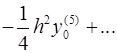
|
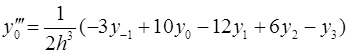
| 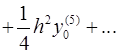
|
Пример 4.2. Функция задана следующей таблицей.
| x | |||||
| y | 1.7475649 | 4.1428558 | 7.4540643 | 13.888067 | 28.290145 |
Вычислить значение производной в точке х=2 по одной из приведенных в табл. 4.1 формул.
Решение. Выберем формулу, содержащую 5 точек таблицы.
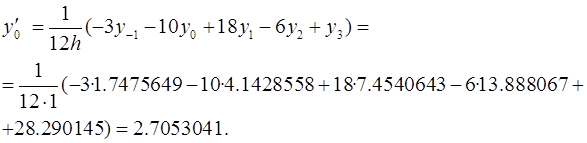
Дата добавления: 2022-02-05; просмотров: 609;











