Обобщенные формулы прямоугольников, трапеций и Симпсона

Из рисунков 5.1- 5.5 видно, что чем больше длина отрезка [a, b], тем, как правило, больше погрешность, то есть разность между точным значением интеграла и приближенным, полученным по соответствующей квадратурной формуле. Для уменьшения этой погрешности поступают следующим образом. Отрезок [a, b] разбивается на n частей. Для простоты будем считать, что эти части равные, то есть 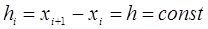. На каждом из отрезков [x_i, x_i+1] используется соответствующая формула. Получают так называемые обобщенные формулы.

Обобщенная формула левых прямоугольников (рис. 5.6).

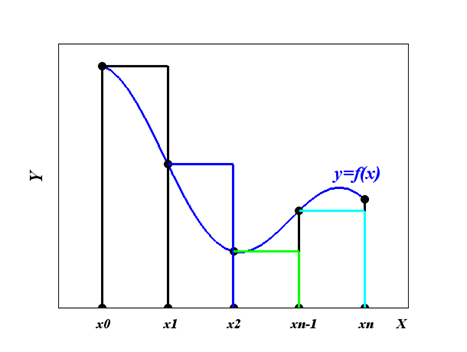
Рис. 5.6. Геометрическая интерпретация обобщенной формулы левых прямоугольнков

Если вычислить сумму площадей каждого получившегося прямоугольника, получим:

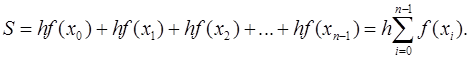
Здесь x₀=a, x_n=b, x_i+1=x_i+h.

Таким образом,

Эту формулу нетрудно запрограммировать.

Обобщенная формула правых прямоугольников

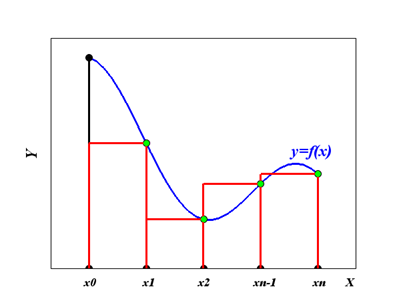
Рис. 5.7. Геометрическая интерпретация обобщенной формулы правых прямоугольнков

Если вычислить сумму площадей всех получившихся прямоугольников, получим:

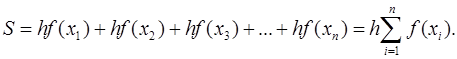
Таким образом,

Обобщенная формула центральных прямоугольников. Для ее применения нам понадобится другая таблица.

Высотой каждого прямоугольника является значение функции в середине каждого из отрезков [x_i, x_i+1].

Если вычислить сумму площадей всех получившихся прямоугольников, получим:

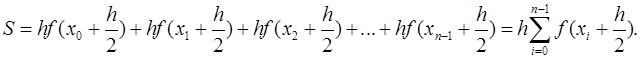
Таким образом,

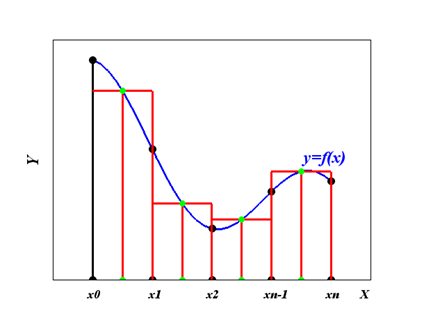
Рис. 5.8. Геометрическая интерпретация обобщенной формулы центральных прямоугольнков

Обобщенная формула трапеций.

Осуществив линейную интерполяцию подынтегральной функции на каждом из отрезков [x_i, x_i+1], получим:

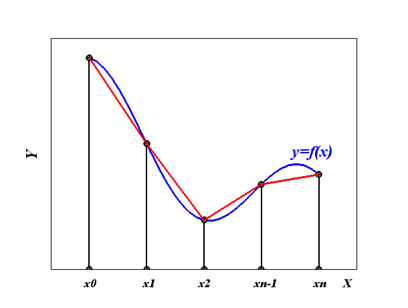
Рис. 5.9. Геометрическая интерпретация обобщенной формулы трапеций

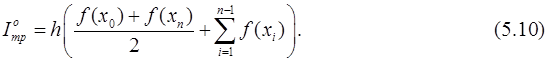
Заменив подынтегральную функцию на параболу второй степени на каждом из отрезков [x_i, x_i+2] и вычислив сумму площадей получившихся криволинейных трапеций аналогично тому, как это было сделано на с. 73, получим обобщенную формулу Симпсона:

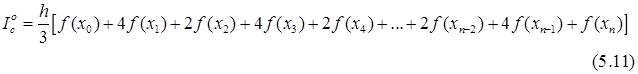
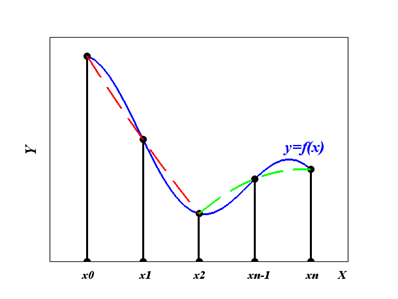
Рис. 5.10. Геометрическая интерпретация обобщенной формулы Симпсона

Первая парабола проходит через три точки с координатами (x₀, f(x₀)), (x₁, f(x₁)) и (x₂, f(x₂)), вторая – через точки (x₂, f(x₂)), (x₃, f(x₃)) и (x₄, f(x₄)), последняя – через точки (x_n-2, f(x_n-2)), (x_n-1, f(x_n-1)) и (x_n, f(x_n)). Число точек в формуле Симпсона должно быть нечетным. Чем больше n, тем, как правило, меньше погрешность E(f). Формулы дают следующую погрешность. Погрешность обобщенных формул левых и правых прямоугольников не превышает величины 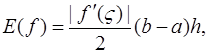погрешность обобщенной формулы центральных прямоугольников – величины 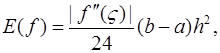погрешность обобщенной формулы трапеций – 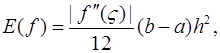погрешность обобщенной формулы Симпсона – не превышает 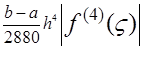[1]. Здесь 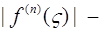максимальное значение модуля соответствующей производной на интервале интегрирования [a, b].

Пример 5.1. Разбив интервал интегрирования на 10 равных частей, вычислить определенный интеграл 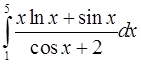по обобщенным формулам прямоугольников, трапеций и Симпсона. Составить программы вычисления этого интеграла по указанным формулам в среде Scilab.

Решение. Всю вычислительную работу проведем в Excel.

Шаг в таблице равен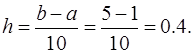

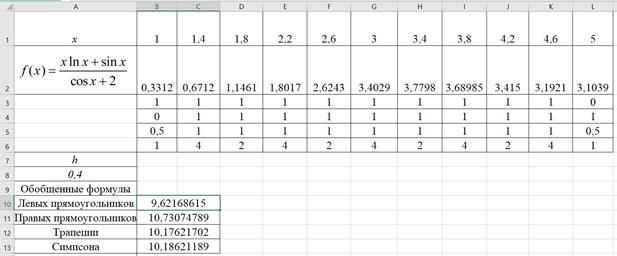
В ячейки B3-L6 введены коэффициенты соответствующих квадратурных формул. Для облегчения расчетов воспользуемся математической функцией СУММПРОИЗВ. Так, в ячейку В13 для вычисления интеграла по обобщенной формуле Симпсона, введена формула

Для вычисления интеграла по обобщенной формуле центральных прямоугольников нам понадобится другая таблица:

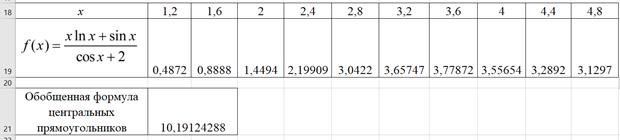
В ячейку В21 введена формула