Формулы прямоугольников, трапеций и Симпсона
Существует несколько формул прямоугольников: формула левых прямоугольников, формулы правых и центральных прямоугольников.
В формуле левых прямоугольников на интервале интегрирования – отрезке [a, b] – подынтегральную функцию 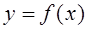 заменяют прямой
заменяют прямой 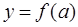 и считают, что интеграл (то есть площадь криволинейной трапеции, ограниченной осью Х, прямыми х=а , х=b и графиком функции
и считают, что интеграл (то есть площадь криволинейной трапеции, ограниченной осью Х, прямыми х=а , х=b и графиком функции 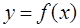 ) приближенно равен площади прямоугольника, основанием которого является отрезок [a, b], а высотой f(a) – значение подынтегральной функции в точке а:
) приближенно равен площади прямоугольника, основанием которого является отрезок [a, b], а высотой f(a) – значение подынтегральной функции в точке а:
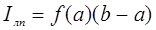 (5.2)
(5.2)
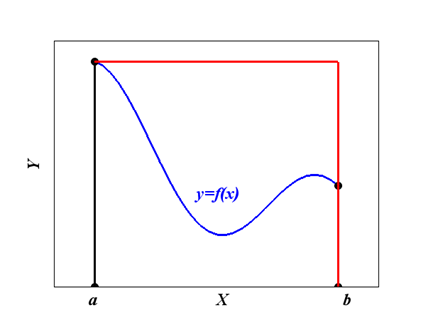
Рис. 5.1. Геометрическая интерпретация формулы левых прямоугольников
В формуле правых прямоугольников на отрезке [a, b] функцию y=f(x) заменяют прямой y=f(b) и считают, что интеграл приближенно равен площади прямоугольника, основанием которого является отрезок [a, b], а высотой f(b) – значение подынтегральной функции в точке b:
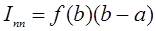 (5.3)
(5.3)
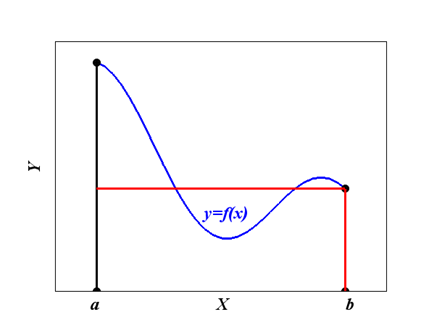
Рис. 5.2. Геометрическая интерпретация формулы правых прямоугольников
В формуле центральных прямоугольников на отрезке [a, b] функцию 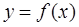 заменяют прямой
заменяют прямой 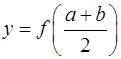 и считают, что интеграл приближенно равен площади прямоугольника, основанием которого является отрезок [a, b], а высотой значение функции в точке
и считают, что интеграл приближенно равен площади прямоугольника, основанием которого является отрезок [a, b], а высотой значение функции в точке 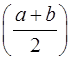 :
:
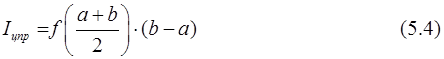
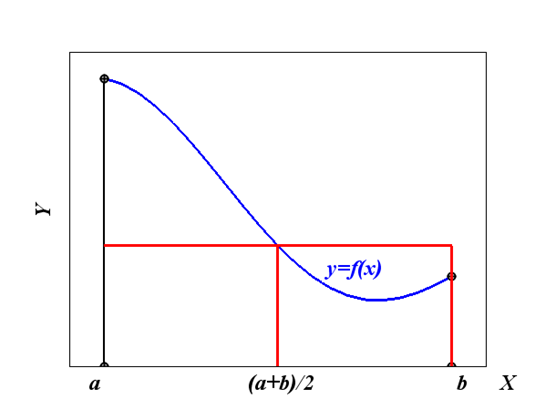
Рис. 5.3. Геометрическая интерпретация формулы центральных прямоугольников
В формуле трапеций на отрезке [a, b] функцию y=f(x) заменяют полиномом первой степени – прямой, проходящей через точки с координатами (a, f(a)) и (b, f(b)) – и считают, что интеграл приближенно равен площади прямоугольной трапеции, образованной прямыми x=a, x=b, осью Х и прямой, проходящей через точки (a, f(a)) и (b, f(b)):
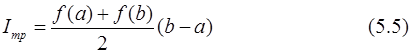
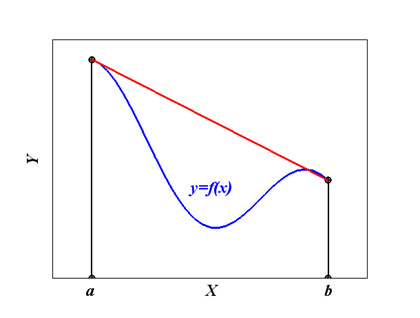
Рис. 5.4. Геометрическая интерпретация формулы трапеций
В формуле Симпсона (формуле парабол) на отрезке [a, b] функцию y=f(x) заменяют полиномом второй степени, проходящим через точки (a, f(a)) , 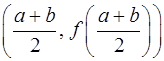 и (b, f(b)) и считают, что интеграл приближенно равен площади криволинейной трапеции, ограниченной осью Х, прямыми x=a, x=b и параболой, проходящей через указанные точки:
и (b, f(b)) и считают, что интеграл приближенно равен площади криволинейной трапеции, ограниченной осью Х, прямыми x=a, x=b и параболой, проходящей через указанные точки:
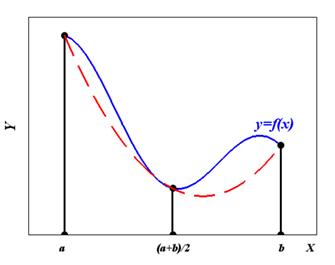
Рис. 5.5. Геометрическая интерпретация формулы Симпсона
Покажем, как выводится формула Симпсона. Запишем уравнение параболы, проходящей через три точки (a, f(a)) , 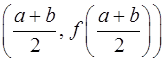 и (b, f(b)), используя формулу интерполяционного полинома Ньютона второй степени:
и (b, f(b)), используя формулу интерполяционного полинома Ньютона второй степени:
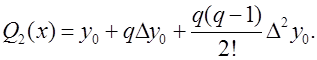
Здесь
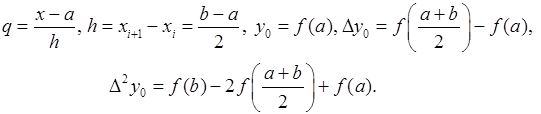
Площадь искомой криволинейной трапеции S равна
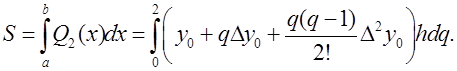
Здесь мы сделали замену переменной интегрирования.
Отсюда
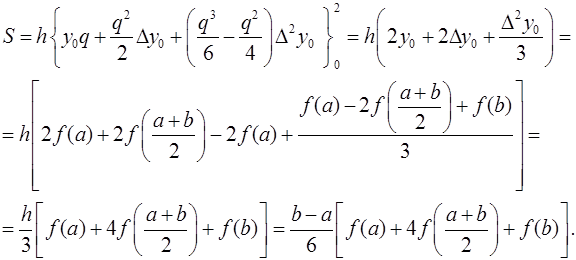
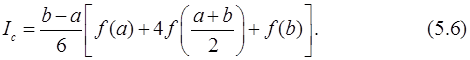
Дата добавления: 2022-02-05; просмотров: 505;











