Построение интерполяционных полиномов

3.3.1.1. Построение таблицы конечных разностей

Покажем, как в Scilab можно построить таблицу конечных разностей, используемую для вычислений с помощью интерполяционных полиномов Ньютона. Для примера 3.2 это можно сделать так.

clc;y=[78.03 89.02 98.91 107.76 115.62];

dy=diff(y),dy2=diff(y,2),dy3=diff(y,3),dy4=diff(y,4)

disp('y=',y,'dy2=',dy2,'dy3=',dy3,'dy4=',dy4)

Результаты работы программы:

"y=" 78.03 89.02 98.91 107.76 115.62

"dy=" 10.99 9.89 8.85 7.86

"dy2=" -1.1 -1.04 -0.99

"dy3= 0.06 0.05

"dy4=" -0.0100000

3.3.1.2. Нахождение коэффициентов интерполяционных полиномов

Покажем, как можно было решить пример 3.2 в Scilab. В приведенной ниже программе значения коэффициентов получаются в результате решения системы из 5 линейных уравнений (полином проходит через 5 точек таблицы).

clc;clf()

x =[498 598 698 798 898];

y = [78.03 89.02 98.91 107.76 115.62];

n=length(x);a=[];b=[];c=[];

for i=1:n

for j=1:n

a(i,j)=sum(x.^(i+j-2));

end

b(i)=sum(x.^(i-1).*y);

end

c=inv(a)*b

function z=f(t)

z=0;

for i=1:n

z=z+t.^(i-1).*c(i);

end

endfunction

plot2d(x,y,-4)

t=min(x):0.1:max(x)+.1;plot2d(t,f(t),1);aa=gca();

aa.data_bounds=[min(x)-0.1 77;max(x)+0.1 116];

gca.children.children.thickness=3

r=[870 522];z1=f(r),plot(r,z1,"*");err=sum((y-f(x)).^2)

legend('Исходные данные','Интерполяционный полином', 'Решение задачи интерполяции',5)

gca.children(1).font_style = 5; gca.children(1).font_size = 3;

gca.children.children(1).polyline_style = 3; gca.children.children(1).thickness = 3;

disp(' T Cp' ;[r;z1]', 'err=' ,err, 'c=' ,c)

Строится полином четвертой степени, проходящий через пять заданных точек. Строится график полученной кривой, на который наносятся и исходные данные. Вычисляется значение интерполяционного полинома в заданных точках r (переменная z1). Решения задачи интерполяции (значения функции в заданных точках Т=522 и Т=870) также наносятся на график.

Результаты работы программы:

" T Cp"

870. 113.51649

522. 80.7715

"c="

4.15075

0.1852081

-0.0000833

2.080D-08

-4.167D-12

"err=" 1.840D-12

Коэффициенты полинома равны элементам вектора c (в порядке возрастания степеней). Правильность решения контролируется переменной err, которая должна принимать значение, близкое к нулю.

На рис.3.8 приведен график получившегося полинома.

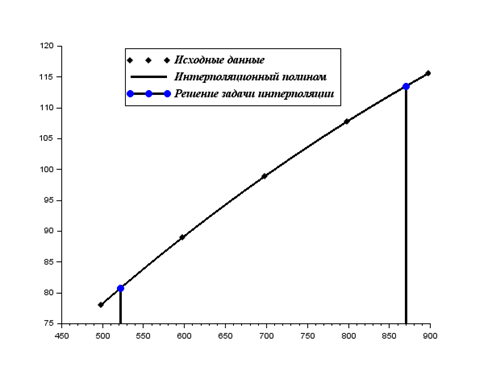
Рис. 3.8. Графическое решение задачи интерполяции по условиям примера 3.2

Замечание. Практика показала, что использование функции datafit при решении задачи интерполяции, когда степень аппроксимирующего полинома велика, в некоторых случаях дает неверные результаты.