Вопрос 2. Соотношения неопределенностей Гейзенберга.
Физические величины никогда не могут быть измерены абсолютно точно. Измеренное значение любой физической величины всегда отличается от ее истинного значения, которое всегда неизвестно, так как при выполнении любого измерения неизбежна ошибка. Источников ошибок много. Они связаны с несовершенством измерительных приборов, с изменением условий опыта, с неполнотой теоретической модели и приближенным характером используемого метода измерений, с округлением при вычислениях и т.д.
Поэтому необходимым условием выполнения любого измерения является нахождение некоторого интервала значений, в который с высокой вероятностью должно попасть истинное значение измеряемой величины. Измерение, например, координаты 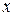 материальной точки должно сопровождаться определением ошибки измерения
материальной точки должно сопровождаться определением ошибки измерения 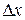 , измерение компоненты импульса
, измерение компоненты импульса 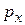 - определением ошибки
- определением ошибки 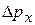 .
.
В классической физике не было принципиальных ограничений на точность измерений. Считалось, что при достаточно совершенной аппаратуре все величины, характеризующие физическую систему, могут быть измерены со сколь угодно высокой точностью.
Однако для микроскопических систем неограниченное повышение точности получается не всегда. В некоторых случаях существуют принципиальные ограничения на точность измерений. Эти ограничения не определяются совершенством измерительной аппаратуры. Каждое из этих ограничений является фундаментальным свойством материи. Проявляются эти свойства только в микромире.
Принципиальные ограничения на точность измерений физических величин называются соотношениями неопределенностей.
Впервые соотношения неопределенностей были сформулированы немецким физиком Гейзенбергом в 1927 г.
Наиболее важными являются два соотношения неопределенностей. Первое устанавливает ограничения на точность одновременного определения координат частицы и соответствующих компонентов ее импульса. Для 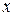 - координаты это соотношение записывается в виде
- координаты это соотношение записывается в виде
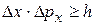 (20.4)
(20.4)
(при строгом применении формализма квантовой механики получается соотношение 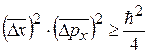 , однако для качественных оценок используют именно выражение (20.4)).
, однако для качественных оценок используют именно выражение (20.4)).
Второе соотношение устанавливает предел точности измерения энергии за данный промежуток времени
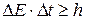 , (20.5)
, (20.5)
где 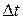 - длительность измерения энергии,
- длительность измерения энергии, 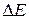 - неопределенность энергии.
- неопределенность энергии.
Соотношения неопределенностей обусловлены корпускулярно-волновым дуализмом.
В качестве примера рассмотрим движение свободного электрона в пространстве. Его движение описывается с помощью плоской монохроматической волны, которая обладает строго определенными значениями частоты и волнового вектора. При этом сопоставляемая электрону волна занимает все пространство и имеет неограниченное время существования. Докажем, что одновременное «точное» определение координаты и импульса электрона невозможно.
Результат прохождения световой волны через щель хорошо известен из оптических экспериментов. На экране наблюдается дифракционная картина в виде чередующихся светлых и темных полос. Можно предположить, что и прохождение электронной волны через щель приведет к аналогичным результатам.
Так как движения микрочастиц описываются либо с волновых, либо с корпускулярных позиций, то рассмотрим результаты дифракции электронов с более привычной корпускулярной точки зрения.
Пусть до щели все электроны двигались параллельно оси 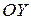 с одинаковыми импульсами
с одинаковыми импульсами 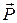 (рис. 20.6).
(рис. 20.6).
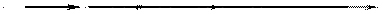
Рис.20.6
Одинаковые значения импульсов электронов можно получить, разгоняя их в электрическом поле, а затем производя селекцию по скоростям. Однако о положении каждого электрона ничего определенного сказать нельзя. Координата 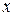 электронов до щели совершенно не определена. Поэтому, в каком месте экрана
электронов до щели совершенно не определена. Поэтому, в каком месте экрана 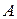 окажется тот или иной электрон заранее предсказать невозможно. На экране
окажется тот или иной электрон заранее предсказать невозможно. На экране 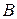 получается дифракционная картина, аналогичная дифракции световой волны на щели. Она свидетельствует о том, что некоторые электроны прошли через щель в экране
получается дифракционная картина, аналогичная дифракции световой волны на щели. Она свидетельствует о том, что некоторые электроны прошли через щель в экране 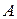 . Пусть ширина щели
. Пусть ширина щели 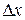 . Эта щель представляет собой своеобразный измерительный прибор, с помощью которого можно определить в плоскости экрана
. Эта щель представляет собой своеобразный измерительный прибор, с помощью которого можно определить в плоскости экрана 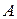 координату прошедшего электрона с точностью
координату прошедшего электрона с точностью 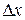 . Возникновение на экране
. Возникновение на экране 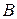 дифракционной картины с корпускулярной точки зрения следует трактовать, как отклонение каждого электрона, прошедшего через щель, на некоторый угол
дифракционной картины с корпускулярной точки зрения следует трактовать, как отклонение каждого электрона, прошедшего через щель, на некоторый угол 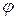 от направления своего первоначального распространения, причём импульс электрона
от направления своего первоначального распространения, причём импульс электрона 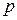 по абсолютной величине остается неизменным. Каждый электрон после прохождения через щель приобретет составляющую импульса
по абсолютной величине остается неизменным. Каждый электрон после прохождения через щель приобретет составляющую импульса 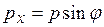 . Причём
. Причём 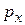 меняется непредсказуемым образом от 0 (электрон вообще не отклонился от направления своего первоначального распространения) до
меняется непредсказуемым образом от 0 (электрон вообще не отклонился от направления своего первоначального распространения) до 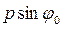 (угол
(угол 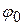 соответствует первому дифракционному минимуму). Часть электронов будет отклоняться на углы, большие чем
соответствует первому дифракционному минимуму). Часть электронов будет отклоняться на углы, большие чем 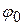 , однако этим числом можно пренебречь по сравнению с количеством электронов, отклоняющихся в пределах центрального максимума. Таким образом, появляется неопределенность
, однако этим числом можно пренебречь по сравнению с количеством электронов, отклоняющихся в пределах центрального максимума. Таким образом, появляется неопределенность 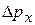 в нахождении проекции импульса на ось
в нахождении проекции импульса на ось 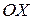
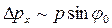 . (20.6)
. (20.6)
В оптике дифракционных явлений известно, что при падении на щель шириной 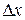 монохроматической волны длиной
монохроматической волны длиной 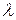 , первый минимум интенсивности света появляется под углом
, первый минимум интенсивности света появляется под углом 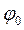 , для которого выполняется соотношение:
, для которого выполняется соотношение: 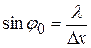 . Выражение (20.6) с учетом этого соотношения запишется в виде:
. Выражение (20.6) с учетом этого соотношения запишется в виде: 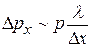 . Используя формулу де Бройля
. Используя формулу де Бройля 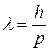 , получим:
, получим:
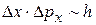 . (20.7)
. (20.7)
Увеличивая ширину щели 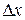 , можно уменьшить неопределенность
, можно уменьшить неопределенность 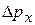 в нахождении проекции импульса на ось
в нахождении проекции импульса на ось 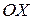 и, наоборот, уменьшая неопределенность в нахождении координаты электрона (уменьшая ширину щели
и, наоборот, уменьшая неопределенность в нахождении координаты электрона (уменьшая ширину щели 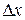 ) увеличиваем неопределенность
) увеличиваем неопределенность 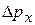 . Одновременное с заранее заданной точностью определение координаты
. Одновременное с заранее заданной точностью определение координаты 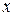 и проекции импульса электрона
и проекции импульса электрона 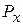 вследствие наличия у электрона волновых свойств, невозможно.
вследствие наличия у электрона волновых свойств, невозможно.
Таким образом, предел ошибок (неопределенностей) 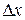 и
и 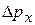 , с которыми состояние микрочастицы можно характеризовать классически, то есть координатой
, с которыми состояние микрочастицы можно характеризовать классически, то есть координатой 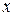 и импульсом
и импульсом 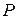 , определяется соотношением неопределенностей Гейзенберга (20.4). В частном случае неопределенности
, определяется соотношением неопределенностей Гейзенберга (20.4). В частном случае неопределенности 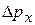 может и не быть. Так было при движении электронов до экрана
может и не быть. Так было при движении электронов до экрана 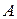 . Но тогда, согласно соотношению неопределенностей,
. Но тогда, согласно соотношению неопределенностей, 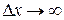 . Это означает, что частица может быть с равной вероятностью обнаружена в любом месте экрана
. Это означает, что частица может быть с равной вероятностью обнаружена в любом месте экрана 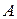 .
.
Следует особо отметить роль постоянной Планка 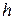 в соотношениинеопределенностей. Отличие
в соотношениинеопределенностей. Отличие 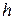 от нуля исключает обращение в нуль
от нуля исключает обращение в нуль 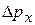 при заданном значении
при заданном значении 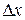 . Только переход к классической физике, в которой
. Только переход к классической физике, в которой 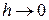 , снимает ограничения на точность измерений.
, снимает ограничения на точность измерений.
При произвольном движении частицы в пространстве соотношения неопределенностей выражаются тремя неравенствами:
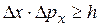 ,
, 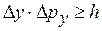 ,
, 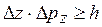 . (20.8)
. (20.8)
Рассмотрим несколько примеров:
1). Электрон движется со скоростью V=103 м/с. Пусть егоскорость определена с точностю ΔV/V=0,10/0. Чему равна неопределенность положения электрона?
Из соотношения (5.4) имеем: 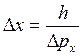 , но
, но 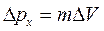 , тогда
, тогда 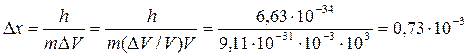 м = 0,73 мм,
м = 0,73 мм,
хотя размер атомов или молекул ≈ 10-10 м. Т.е. неопределенность в определении координаты Δx значительно больше размеров самого атома. Здесь электрон − классическая частица. Такая точность достаточна, чтобы можно было говорить о движении электронов по определенной траектории, иными словами, описывать их движения законами классической механики.
2). Пуля массой 10 г вылетает из винтовки со скоростью V = 103 м/c. Пусть ΔV/V=0,10/0. Чему равна неопределенность положения пули?
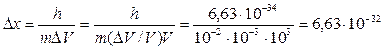 м.
м.
Т.е. неопределенность в определении координаты Δx значительно меньше размеров пули. Здесь пуля − классическая частица. Ее координата определяется точно.
3). Применим соотношение неопределенностей к электрону, движущемуся в атоме водорода. Допустим, что неопределенность координаты электрона Δx ≈10-10 м (порядка размеров самого атома), тогда, согласно (20.4),
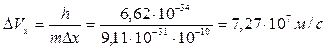 .
.
Используя законы классической физики, можно показать, что при движении электрона вокруг ядра по круговой орбите радиуса r ≈ 0,5⋅10-10 м его скорость V ≈ 2,3⋅106 м/с. Таким образом, неопределенность скорости в несколько раз больше самой скорости.Очевидно, что в данном случае нельзя говорить о движении электронов в атоме по определенной траектории. Иными словами, для описания движения электронов в атоме нельзя пользоваться законами классической физики.
Теперь обоснуем соотношение неопределенностей (5.5) для энергии и времени. Для волнового пакета (группы волн) справедливо соотношение:
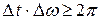 , (20.9)
, (20.9)
смысл которого заключается в том, что ограниченный во времени волновой процесс не может быть монохроматическим. Если процесс длится в течение времени 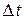 , то разброс частот
, то разброс частот 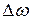 (и соответственно разброс длин волн) удовлетворяет соотношению (20.9). Поэтому если для наблюдения даже монохроматического процесса предоставлено некоторое время
(и соответственно разброс длин волн) удовлетворяет соотношению (20.9). Поэтому если для наблюдения даже монохроматического процесса предоставлено некоторое время 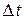 , то частота процесса может быть определена лишь с ошибкой
, то частота процесса может быть определена лишь с ошибкой 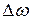 , подчиняющейся соотношению (20.9). Так как
, подчиняющейся соотношению (20.9). Так как 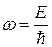 , то соотношение (20.9) принимает вид:
, то соотношение (20.9) принимает вид: 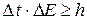 .
.
Это означает, что чем меньше время 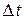 отведено для определения энергии микрообъекта, тем с меньшей неопределенностью можно говорить об энергии этого состояния. Электрон в стационарном состоянии атома может находиться сколь угодно долго (
отведено для определения энергии микрообъекта, тем с меньшей неопределенностью можно говорить об энергии этого состояния. Электрон в стационарном состоянии атома может находиться сколь угодно долго ( 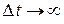 ), поэтому энергия стационарного состояния имеет вполне определенное значение (
), поэтому энергия стационарного состояния имеет вполне определенное значение ( 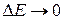 ) .
) .
Принцип неопределенностей − фундаментальный принцип квантовой механики, устанавливающий физическое содержание и структуру ее математического аппарата. Многие результаты задач, рассматриваемых в квантовой механике, могут быть получены и поняты на основе комбинации законов классической механики с соотношением неопределенностей. Важный тому пример − проблема устойчивости атома. Рассмотрим эту задачу для атома водорода.
Пусть электрон движется вокруг ядра по круговой орбите радиуса r
со скоростью V. По закону Кулона сила притяжения электрона к ядру уравновешивается центробежной силой 
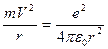 , где m − масса электрона, ε0 − электрическая постоянная, тогда радиус его орбиты
, где m − масса электрона, ε0 − электрическая постоянная, тогда радиус его орбиты 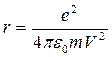 может быть сколь угодно малым, если скорость V достаточно велика. Но в квантовой механике должно выполняться соотношение неопределенностей.
может быть сколь угодно малым, если скорость V достаточно велика. Но в квантовой механике должно выполняться соотношение неопределенностей.
Если допустить неопределенность положения электрона ∆x в пределах радиуса его орбиты r, т.е. ∆x = r, а неопределенность скорости ∆V в пределах V, т.е. ∆p=m∆V=mV, то соотношение неопределенностей примет вид: mVr ≥ ħ. Учитывая связь между V и r, получим 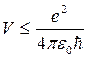 и
и 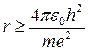 . Следовательно, движение электрона по орбите радиуса r < r0 =
. Следовательно, движение электрона по орбите радиуса r < r0 = 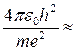 0,5·10-10 м невозможно. Таким образом, электрон не может упасть на ядро, что объясняет устойчивость атома. Величина r0 и является радиусом атома водорода. Ему соответствует энергия связи атома E0 (равная полной энергии электрона в атоме, т.е. сумме кинетической энергии
0,5·10-10 м невозможно. Таким образом, электрон не может упасть на ядро, что объясняет устойчивость атома. Величина r0 и является радиусом атома водорода. Ему соответствует энергия связи атома E0 (равная полной энергии электрона в атоме, т.е. сумме кинетической энергии 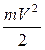 и потенциальной энергии
и потенциальной энергии 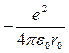 ), что составляет
), что составляет 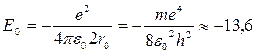 эВ. Это минимальное значение энергии E0 соответствует энергии основного состояния атома водорода.
эВ. Это минимальное значение энергии E0 соответствует энергии основного состояния атома водорода.
Таким образом, квантовомеханические представления впервые дали возможность теоретически оценить размеры атома, выразив его радиус через фундаментальные физические постоянные ħ, m, e, ε0.
Остановимся в заключение на смысле, вкладываемом в понятие «орбита электрона» в атоме. В отличие от теории Бора, в квантовой механике не существует определенныхорбит электрона в атоме. Существование определенных орбит, т.е. точноизвестных расстояний электрона от ядра, противоречит соотношению неопределенностей. Под термином «орбита электрона» в квантовой механике понимается расстояние от ядра, на котором вероятность обнаружить электрон максимальна.
Еще раз подчеркнем, что соотношения неопределенностей не связаны с несовершенством измерительной техники, а являются объективным свойством материи: таких состояний микрочастиц, в которых и координата, и импульс частицы имеют определенное значение, просто не существуетв природе.
Вывод: к волновому и корпускулярному описанию следует относиться как к равноправным и дополняющим друг друга точкам зрения. Рубеж, разделяющий две концепции волн и частиц определяется именно ограниченными возможностями измерения.
Контрольные вопросы:
1. В чем состоит физический смысл волн де Бройля?
2. Каков физический смысл соотношений неопределенностей Гейзенберга?
3. В каком случае и почему можно говорить о движении частицы по определенной траектории?
4. Как, исходя из соотношения неопределенностей, объяснить наличие естественной ширины спектральных линий?
Дата добавления: 2017-10-04; просмотров: 3488;











