Вопрос 4. Теория атома водорода.

Теорию водородоподобного атома обычно называют теорией атома водорода. Прежде, чем её рассматривать, коротко остановимся на свойствах электрона, как элементарной частицы.

Элементарные частицы характеризуются массой, зарядом, величиной собственного момента импульса (спина) и величиной магнитного момента. Существование собственного механического и магнитного моментов у электрона позволяет представить его условно в виде заряженного волчка, вращающегося вокруг собственной оси. При этом в отличие от классического волчка, который может иметь любое значение механического момента, спин электрона имеет только одно вполне определенное значение, равное ћ/2. Соответственно собственный магнитный момент электрона также имеет только одно вполне определенное значение, равное 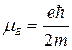= 0,927 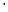10^-23 Дж/Тл, которое получило название магнетона Бора. Знак магнитного момента электрона отрицателен, т.е. его направление противоположно направлению спина. Понятие спина электрона позволило объяснить тонкую структуру атомного излучения, т.е. расщепление уровней энергии и спектральных линий атомов, молекул и кристаллов, обусловленное спин-орбитальным взаимодействием, т.е. взаимодействием собственного механического момента электрона с его орбитальным механическим моментом. Энергия этого взаимодействия зависит от взаимной ориентации орбитального и собственного моментов импульса.

Спином обладают также протоны, нейтроны, фотоны и другие элементарные частицы (кроме мезонов).

Движение электрона относительно ядра представляет собой движение частицы с тремя степенями свободы в кулоновском поле ядра (центральное поле). Потенциальная энергия электрона в таком поле зависит только от расстояния электрона от ядра и не зависит от направления радиус-вектора. Таким образом, имеет место сферическая симметрия. Возможные значения энергии одноэлектронного атома (и соответствующие волновые функции Ψ, характеризующие состояние электрона в нём) получаются при решении уравнения Шредингера. Когда энергия электрона отрицательна (для электрона, связанного с атомом), возможные её значения задаются формулой:

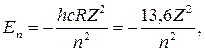
где n = 1, 2, 3… - главное квантовое число, определяющее энергию различных состояний атома, а постоянная hcR (R – постоянная Ридберга) представляет собой энергию ионизации атома водорода, равную энергии его основного состояния (Z = 1, n = 1), взятой с обратным знаком.

В простейшем случае атома водорода расстояния между уровнями энергии (рис. 19.7) закономерно уменьшаются и, бесконечно сгущаясь, уровни сходятся к границе ионизации Е_∞, соответствующей отрыву электрона. Выше границы ионизации лежит непрерывный энергетический спектр. Схема уровней энергии водородоподобных ионов Не⁺, Li²⁺, … отличается от приведённой на рис. 19.7только увеличением масштаба в Z²раз. Для атомов, содержащих два электрона и более, схемы уровней энергии усложняются. На рис. 19.11 показаны стационарные орбиты электронов в водорода и переходы электронов, соответствующие

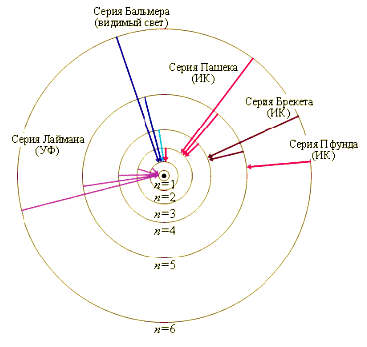
Рис. 19.11

различным спектральным сериям.

Каждый электрон в атоме характеризуется четырьмя квантовыми числами: главным квантовым числом n, принимающим значения n = 1, 2, 3, 4…., азимутальным (орбитальным) l = 0, 1, 2,…n-1, магнитным m_l, принимающим значения (2l+1) значений, и спиновым m_s, принимающим значения +1/2 и -1/2. Состояния с l = 0, 1, 2, 3, 4… принято обозначать

буквами s, p, d, f, g… и соответственно называть s-, p-, d-, f-, g-… состояниями.

Электроны с данным n образуют электронный слой, который состоит из n электронных оболочек с l=0, 1, 2…(n-1) и в соответствии с принципом Паули содержит 2n² электронов (принцип Паули: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых чиселn, l, m_l, m_s). Таким образом, общее число различных состояний с заданными n и l при учёте, что l может принимать значения от 0 до n - 1, равно:

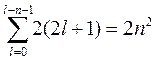. (19.25)

Каждому уровню энергии атома водорода соответствует 2, 8, 18, ..., 2n² (при n = 1, 2, 3, ...) различных стационарных квантовых состояний. Возможные состояния атома водорода при значениях n = 1, 2, 3 приведены на рис. 19.12. Графически показаны ориентации орбитального и спинового моментов.

Если уровню энергии соответствует лишь одно квантовое состояние, то его называют невырожденным, если два или более — вырожденным, а число таких состояний g называется степенью или кратностью вырождения (для невырожденных уровней энергии g = 1). Уровни энергии атома водорода являются вырожденными, а их степень вырождения g_n= 2n².

Квантовое число l = 0, 1, 2, …, n-1 определяет величину орбитального момента атома, т.е. момента импульса электрона M_l относительно ядра:

.

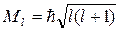При заданном n, число l принимает n различных значений. Состояния с l=0, 1, 2, 3, 4, 5, 6, принято обозначать буквами s, p, d, f, g, h, l,….соответственно.

Квантовое число m_l определяет величину проекции орбитального момента импульса электрона L_z на произвольно выбранное направление z

Рис. 19.12.

при заданном l, при этом число m_l принимает 2l+1 значений: m_l = l, l-1,…,-l. Квантовые числа n, l и m_l полностью характеризуют состояние электрона в атоме, n и l характеризуют размер и форму электронного облака, а квантовое число m_l – ориентациюэлектронного облака в пространстве.

Состояния с l=0, 1, 2, 3, 4, 5, 6, принято обозначать буквами s, p, d, f, g, h, l,….соответственно.

Точное положение электрона в атоме в определённый момент времени установить нельзя вследствие соотношений неопределённостей (Тема 20, пример 3). Состояние электрона в атоме определяется волновой функцией Ψ, которая при заданных значениях n, l и m_l определённым образом зависит от координат; |Ψ|² – плотность вероятности нахождения электрона в данной точке пространства. Таким образом, состояние электрона в атоме можно охарактеризовать распределением в пространстве его электрического заряда с некоторой плотностью. Распределение электронной плотности е|Ψ|² определяет плотность вероятности нахождения электрона в данной точке пространства.

На рис. 19.15 показано угловое f(θ) = e|Ψ|² распределение электронной плотности для состояний атома водорода с разными значениями квантовых чисел n, l, m_l.

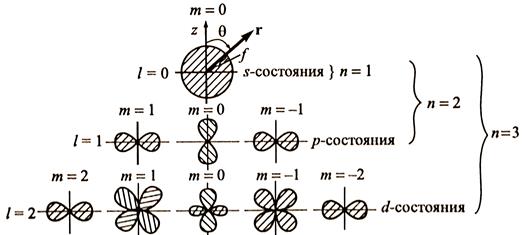
Рис. 19.13.

На рисунке видно, что распределение электронной плотности для состояний с заданным главным квантовым числом n, но с разными значениями орбитального l и магнитного m_l квантовых чисел существенно различаются, хотя согласно формуле (19.15) им соответствуют одинаковые значения энергии. Для n = 2 масштаб рисунка уменьшен в 4 раза, а для n = 3 – в 9 раз, т.к. радиус электронной орбиты в соответствии с формулой (19.11) пропорционален n².

При этом электроны как бы размазаны в пространстве и образуют электронное облако, размеры которого растут пропорционально n². Для s-состояний (l=0) волновая функция и распределение электронной плотности обладают сферической симметрией и обращаются в нуль на (n-1)-й сфере, т.е. имеют n-1 узловую сферическую поверхность; при этом в центре (начале координат) Ψ и |Ψ|² отличны от нуля, что является характерной особенностью s-состояний; в точке, где находится ядро, вероятность нахождения электрона не равна нулю. Для р-состояний (l=1) и d-состояний (l=2) значение волновой функции и распределение электронной плотности в разных направлениях различны и зависят от абсолютного значения m_l; при этом Ψ и |Ψ|² обращаются в нуль на некоторых узловых поверхностях и всегда равны нулю в начале координат.

Независимость энергии атома от m_l (вырождение по m_l) связана со сферической симметрией атома – энергия атома не зависит от значения проекции орбитального момента на произвольное направление, а независимость энергии от l (вырождение по l) связана с тем, что электрон в атоме движется в кулоновском поле ядра.

Для объяснения некоторых явлений (например, тонкой структуры в атомных спектрах) был введён (уравнением Дирака) собственный момент импульса электрона – его спин, существование которого подтвердилось экспериментально опытом Штерна-Герлаха. Со спином электрона связывают спиновый магнитный момент электрона. Проекция спинового момента электрона в атоме на произвольную ось определяется магнитным спиновым (или спиновым) квантовым числом m_s. Таким образом, при заданных l и m_l возможны два различных состояния атома, отличающихся значениями m_s. Полная кратность вырождения по l, m_l и m_s равна 2n².

Для уровней энергии с n ≥ 2 вырождение снимается вследствие влияния спина на орбитальное движение электрона в атоме – спин-орбитального взаимодействия – магнитного взаимодействия магнитного момента электрона с его орбитальным магнитным моментом, возникающим в результате орбитального движения электрона. Снятие вырождения приводит к расщеплению уровней энергии – появлению их тонкой структуры.

Решение уравнений квантовой механики с учётом спина электрона (релятивисткая квантовая механика) приводит к увеличению энергии электрона на некоторую величину.

Наряду с тонкой, наблюдается сверхтонкая структура уровней энергии, обусловленная взаимодействием магнитных моментов электрона с магнитным моментом ядра, а также изотопическое смещение, связанное с различием масс ядер изотопов одного элемента. Изучение всех этих малых эффектов спектроскопическими методами позволяет определять свойства и структуру атомных ядер.