Вопрос 1. Гипотеза де Бройля и ее экспериментальное подтверждение.

В 1924 г. французский физик де Бройль высказал смелую гипотезу о сходстве между светом и частицами вещества: если свет обладает корпускулярными свойствами, то и материальные частицы, в свою очередь, должны обладать волновыми свойствами. Движение электрона или какой–либо другой частицы связано с волновым процессом, т.е. с любой частицей вещества связана некоторая волна, точно так же, как с фотоном связана световая волна. Эти волны не являются электромагнитными. Они имеют специфическую природу, для которой нельзя найти аналогию в классической физике. Движению любой частицы, обладающей импульсом 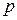, сопоставляется волновой процесс с длиной волны:

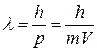. (20.1)

Это выражение называется длиной волны де Бройля для материальной частицы.

Вначале гипотеза де Бройля казалась неправдоподобной из-за отсутствия опытных фактов, подтверждающих существование волновых свойств частиц. Существование волн де Бройля может быть установлено лишь на основе опытов, в которых проявляется волновая природа частиц. Так как волновая природа света проявляется в явлениях дифракции и интерференции, то для частиц, обладающих по гипотезе де Бройля волновыми свойствами, должны также обнаруживаться эти явления.

Трудности наблюдения волновых свойств частиц были связаны с тем, что в макроскопических явлениях эти свойства не проявляются. Например, движению камня массой 1 кг, скорость которого 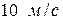, можно сопоставить волновой процесс с длиной волны

.

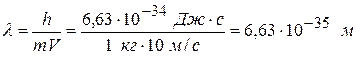Зафиксировать такую короткую длину волны не удается ни в одном из опытов. Однако если рассматривать электроны, масса которых очень мала, то длина волны станет достаточной для ее экспериментального обнаружения. В 1927 г. гипотеза де Бройля была подтверждена экспериментально в опытах американских физиков Дэвиссона и Джермера.

Как известно, при дифракции световых волн дифракционная картина особенно просто получается, когда размеры неоднородностей, на которых происходит дифракция, не слишком велики по сравнению с длиной волны.

Простые расчеты показывают, что длины волн, связанных с частицами, должны быть очень малы, т.е. значительно меньше длин волн видимого света. Поэтому дифракцию частиц можно было обнаружить не на обычной дифракционной решетке для видимого света (с постоянной решетки 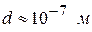), а на кристаллах, атомы в которых расположены в определенном порядке на расстояниях друг от друга ≈ .

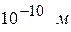Вот почему в своих опытах Дэвиссон и Джермер изучали отражение электронов от монокристалла никеля, принадлежащего к кубической системе.

Схема опыта представлена на рис. 20.1. В вакууме узкий пучок моноэнергетических электронов, получаемый с помощью электронно-лучевой трубки 1, направлялся на мишень 2 (поверхность монокристалла никеля, сошлифованная перпендикулярно к большой диагонали кристаллической ячейки). Отраженные электроны улавливались детектором 3, соединенным с гальванометром. Детектором, который можно было устанавливать под любым углом относительно падающего луча, улавливались только те электроны, которые испытывали упругое отражение от кристалла. По силе электрического тока в гальванометре судили о количестве электронов, зарегистрированных детектором. Оказалось, что при отражении электронных пучков от поверхности металла наблюдается картина, которую невозможно предсказать на основе классической теории. Число электронов, отраженных в некоторых направлениях, оказалось больше, а в некоторых меньше, чем следовало ожидать. То есть возникало избирательное отражение в определенных направлениях. Особенно интенсивно рассеяние электронов происходило под углом 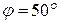при ускоряющем напряжении 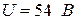. Объяснить результаты эксперимента оказалось возможным лишь на основе волновых представлений об электронах.

Атомы никеля, расположенные на шлифованной поверхности, образуют регулярную отражательную дифракционную решетку. Ряды

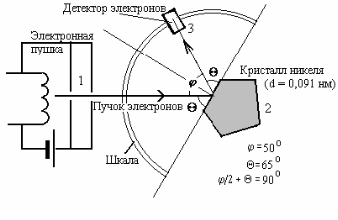
Рис. 20.1

атомов перпендикулярны плоскости падения. Расстояние между рядами d=0,091нм. Эта величина была известна из рентгенографических исследований. Энергия электронов невелика и они не проникают глубоко в кристалл, поэтому рассеяние электронных волн происходит на поверхностных атомах никеля. В некоторых направлениях рассеянные от каждого атома волны усиливают друг друга, в других – происходит их гашение. Усиление волн произойдет в тех направлениях, в которых разность расстояний от каждого атома до точки наблюдения равняется целому числу длин волн (рис. 20.2).

Рис.20.2

Для бесконечно удалённой точки условие усиления рассеянных волн запишется в виде 2dsinθ = nλ (формула Бреггов, n − порядки дифракционных максимумов). Для 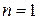и значения угла дифракции 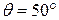соответствует длина волны

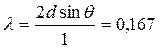нм. (20.2)

Поэтому движение каждого электрона можно описать с помощью волны с длиной 0,167 нм.

Формула де Бройля (20.1) приводит к такому же результату для длины волны. Электрон, ускоренный в электрическом поле разностью потенциалов 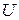, обладает кинетической энергией 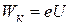. Так как модуль импульса 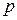частицы связан с ее кинетической энергией 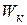соотношением 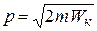, то выражение (20.1) для длины волны можно записать в виде:

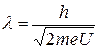. (20.3)

Подставив в (20.3) численные значения величин, получим:

.

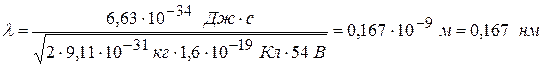Оба результата хорошо совпадают, что подтверждает наличие волновых свойств у электронов.

Таким образом, опыты Дэвиссона и Джермера явились блестящим подтверждением идеи де Бройля о том, что движение электрона или какой–либо другой частицы связано с волновым процессом.

В 1927 г. волновые свойства электронов были подтверждены в независимых экспериментах Томсона и Тартаковского. Ими были получены дифракционные картины при прохождении электронов через тонкие металлические пленки.

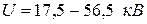В опытах Томсона электроны в электрическом поле разгонялись до больших скоростей при ускоряющем напряжении , что соответствовало длинам волн электронов от 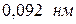до 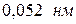(согласно формуле (20.3)). При этом вычисления проводились по релятивистским формулам. Тонкий пучок быстрых электронов направлялся на золотую фольгу толщиной 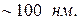Использование быстрых электронов связано с тем, что более медленные электроны сильно поглощаются фольгой. За фольгой помещали фотопластинку (рис.20.3).

Рис.20.3

Действие электронов на фотопластинку аналогично действию быстрых фотонов рентгеновского диапазона при прохождения их через фольгу из алюминия. После продолжительной бомбардировки фольги электронами на фотопластинке образовывалось центральное пятно, окруженное дифракционными кольцами. Происхождение дифракционных колец такое же, как и в случае дифракции рентгеновских лучей.

Другое доказательство дифракции электронов в кристаллах дают сходные снимки электронограммы и рентгенограммы одного и того же кристалла. С помощью этих снимков можно определить постоянную кристаллической решетки. Вычисления, проведенные с помощью двух различных методов, приводят к одинаковым результатам.

Наиболее наглядные экспериментальные результаты, подтверждающие волновую природу электронов, получены в опытах по дифракции электронов на двух щелях (рис. 20.4), выполненных впервые в 1961 г. К. Йёнсоном. Эти опыты – прямая аналогия опыта Юнга для видимого света.

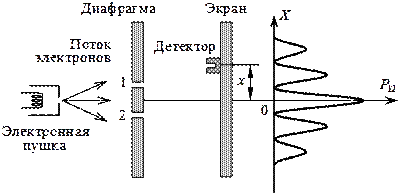
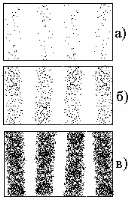
Рис. 20.4 Рис.20.5

Поток электронов, ускоренных разностью потенциалов 40 кВ, после прохождения двойной щели в диафрагме попадал на экран (фотопластинку). В местах попадания электронов на фотопластинке образуются темные пятна. При большом числе электронов на фотопластинке наблюдается типичная интерференционная картина в виде чередующихся максимумов и минимумов интенсивности электронов, полностью аналогичная интерференционной картине для видимого света. Р₁₂ − вероятность попадания электронов в различные участки экрана на расстоянии x от центра. Максимальная вероятность соответствует дифракционному максимуму, нулевая вероятность – дифракционному минимуму

Характерно, что все описанные результаты опытов по дифракции электронов наблюдаются и в том случае, когда электроны пролетают через экспериментальную установку “поодиночке”. Этого можно добиться при очень малой интенсивности потока электронов, когда среднее время пролета электрона от катода до фотопластинки меньше, чем среднее время между испусканием двух последующих электронов с катода. На рис.20.5 показаны фотопластинки после попадания различного числа электронов (экспозиция возрастает от рис. 20.5а к рис. 20.5в). Последовательное попадание на фотопластинку все возрастающего количества одиночных электронов постепенно приводит к возникновению четкой дифракционной картины. Описанные результаты означают, что в данном эксперименте электроны, оставаясь частицами, проявляют также волновые свойства, причем эти волновые свойства присущи каждому электрону в отдельности, а не только системе из большого числа частиц.

Приведенные выше опыты убеждают нас в том, что движению микрочастиц действительно можно сопоставить волновой процесс. Длина волны электрона совпадает с предсказанной формулой де Бройля .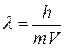

В 1929 г. Штерн и Эстерман показали, что и атомы гелия ( 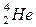) и молекулы водорода ( 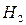) также претерпевают дифракцию. Для тяжелых химических элементов длина волны де Бройля очень мала, поэтому дифракционные картины либо совсем не получались, либо были весьма расплывчатыми. Для легких атомов гелия и молекул водорода средняя длина волны при комнатной температуре порядка 0,1 нм, то есть того же порядка, что и постоянная кристаллической решетки. Пучки этих атомов не проникали вглубь кристалла, поэтому дифракция молекул осуществлялась на плоских двумерных решетках поверхности кристалла, аналогично дифракции медленных электронов на плоской поверхности кристалла никеля ( 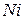) в опытах Дэвиссона и Джермера. В результате наблюдались четкие дифракционные картины. Позднее была обнаружена дифракция на решетках кристаллов очень медленных нейтронов.

В настоящее время техника электронной дифракции достигла столь высокого развития, что в промышленности для определения структуры различных материалов часто пользуются этим методом, вместо старого метода дифракции рентгеновских лучей. А возможность фокусировки электронного пучка с помощью так называемых электронных линз (специально подобранных индукционных катушек и конденсаторов) позволила сконструировать электронный микроскоп.

В 1931г. впервые было получено изображение объекта, сформированное пучками электронов на электронном микроскопе

(М. Кнолль и Е. Руска). К середине 1960–х гг. электронная микроскопия достигла столь высокого технического совершенства, что началось широкое ее применение в научных и технических целях. Электронные микроскопы по своей разрешающей способности превосходят световые микроскопы в несколько тысяч раз. Предел разрешения, характеризующий способность прибора отобразить раздельно две максимально близко расположенные детали объекта, у электронного микроскопа составляет (0,15-0,3) нм, т.е. достигает уровня, позволяющего наблюдать атомарную и молекулярную структуру исследуемых объектов. Столь высокие разрешения достигаются благодаря очень малой длине волны электронов. В последнее время ведутся работы по созданию электронных голографических систем.

Волновые свойства нейтронов используются при исследовании структуры и свойств вещества с помощью рассеяния нейтронов низких энергий ( 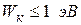). Длина волны де Бройля таких медленных нейтронов (λ ≥ 0,03 нм) соизмерима с межатомными расстояниями в конденсированных средах, что позволяет изучать взаимное расположение атомов (нейтронография).

Отсутствие электрического заряда нейтрона, наличие массы покоя, высокая проникающая способность, возможность обмена со средой значительной частью кинетической энергии, а также взаимодействие с веществом только посредством ядерных и магнитных сил делают нейтронографию, т.е. совокупность методов исследования атомной структуры конденсированных сред при дифракции медленных нейтронов на атомных ядрах, удобным методом для исследования в физике твердого тела, жидкостей, физической химии, молекулярной биологии и др.

Наконец, волновые свойства ионов используются в ионном микроскопе, в котором для получения изображения применяется ионный пучок. Ионный микроскоп по принципу действия аналогичен электронному микроскопу, но по сравнению с ним обладает более высокой разрешающей способностью. Длина волны де Бройля для ионов в 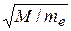раз меньше, чем для электронов ( 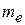- масса электрона, 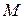- масса иона) при одинаковом ускоряющем напряжении. Вследствие этого в ионном микроскопе очень малы эффекты искажения, обусловленные дифракцией, которые ограничивают в электронном микроскопе его разрешающую способность. Другим преимуществом ионного микроскопа является его высокая контрастность изображения.

К недостаткам ионного микроскопа относятся:

1. заметная потеря энергии ионов даже при прохождении их через очень тонкие объекты, которые быстро разрушаются;

2. разрушение люминофора экрана ионами;

3. слабое фотографическое действие ионов.

Волновые свойства ионов используются в таких приборах, как ионный проектор (ионный микроскоп без линз) и атомный зонд, применяемые для исследования поверхностей веществ. В частности, пространственное разрешение атомного зонда составляет порядка размера атома.

Таким образом, волновые свойства электронов, нейтронов, протонов, ионов и других частиц, а также атомов и молекул не только надежно доказаны прямыми опытами, но и широко используются в установках с высокой разрешающей способностью, так что можно говорить об инженерном использовании волн де Бройля.

В 1929 г. де Бройлю была присуждена Нобелевская премия за открытие волновой природы электрона.

Физический смысл волн де Бройля.Чтобы найти истолкование волнам, связанным с частицами, сравним дифракцию световых волн и дифракцию частиц. Всякая волна представляет собой процесс распространения в пространстве изменений какой-либо величины. В частности, световые волны – это периодические изменения в пространстве напряженностей электрического и магнитного полей. Проходя через какое-либо отверстие, волна испытывает дифракцию. При этом в результате наложения дифрагирующих волн друг на друга происходит усиление или ослабление амплитуды колебаний в различных местах пространства. На фотопластинке, поставленной за отверстием, после проявления обнаруживаются почерневшие места (дифракционные максимумы). Для регистрации частиц вместо фотопластинки используют счетчики частиц. Степень почернения фотопластинки в результате действия световой волны пропорциональна энергии волны, приходящейся на единицу площади в данном месте пластинки. Эта энергия, в свою очередь, пропорциональна квадрату амплитуды волны.

Частицу мы не можем представить себе распределенной в пространстве. Она попадает в какое-то определенное место фотопластинки и вызывает почернение одного зерна фотоэмульсии. Как показывает опыт, попадание отдельных частиц в определенные места пластинки носит случайный характер: иногда несколько частиц подряд может попасть почти в одно и то же место, иногда же они попадают далеко друг от друга. Однако если общее число частиц, попавших на пластинку, велико, то оказывается, что в некоторые места пластинки, а именно в те, где после проявления обнаруживаются темные кольца, частиц попадает больше. Туда же, где расположены светлые кольца, частицы практически не попадают совсем. Можно сказать, что частицы после прохождения через металлическую фольгу на одни участки фотопластинки попадают с большей вероятностью, а на другие – с меньшей. Мерой вероятности в данном случае служит доля частиц, попавших на данный участок, из числа всех попавших на фотопластинку частиц.

Итак, в случае дифракции частиц степень почернения отдельных участков фотопластинки мы связываем с вероятностью попадания частиц на эти участки пластинки. В случае света, как говорилось выше, степень почернения пропорциональна квадрату амплитуды световой волны. Отсюда мы можем сформулировать физический смысл волн де Бройля: квадрат амплитуды волны де Бройля определяет вероятность нахождения частицы в данной области пространства.