Вопрос 3. Применение уравнения Шрёдингера к свободному электрону.

Рассмотрим применение уравнения Шрёдингера к свободной частице, движущейся вдоль оси ОX,например, к свободному электрону, т.е. к электрону, не испытывающему действия внешних полей. В этом случае потенциальная энергия свободно движущейся частицы U = 0, и уравнение Шрёдингера принимает вид:

.

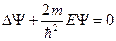Согласно гипотезеде Бройля движение такого микрообъекта моделируется плоской монохроматической волной, занимающей все пространство: 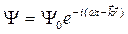. Для свободной частицы, движущейся вдоль оси ОX волновая функция будет иметь следующий вид:

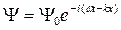, (21.10)

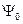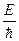
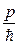где -амплитуда волны. Круговая частота ω и волновое числоk связаны с полной энергией Е и импульсом p соотношениями: Е = ћω; p = ћk, отсюда ω = ; k = . Тогда волноваяфункция(21.10) принимает вид:

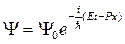. (21.11)

Не зависящая от времени плотность вероятности обнаружения частицы в данной точке пространства 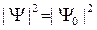означает, что все положения свободной частицы в пространстве являются равновероятными.

Покажем что данный вид 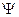- функции удовлетворяет уравнению Шрёдингера (21.4). Для этого:

1). Найдем ∆ 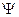и выразим p²:

,

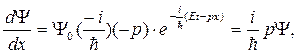
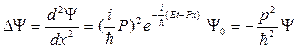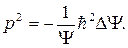(21.12)

2). Найдем 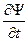и из полученного выражения определим энергию Е:

.

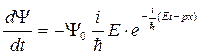
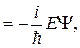
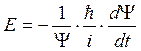3). Подставим значения Е и p в соотношение = :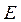

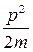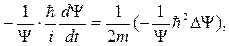
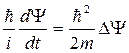, или

­− .

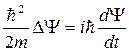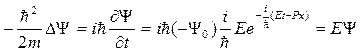
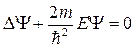→ . Полученное соотношение совпадает с уравнением Шрёдингера (21.7) для случая U=0.

Собственным значением энергии волновой функции (21.10), (21.11) является .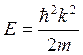

Так как волновое число k может принимать любые значения k > 0, то и энергия свободной частицы может принимать любые значения, следовательно, ее энергетический спектр является непрерывным.

Обоснуем справедливость вида волновой функции (21.10) и для случая движения частицы в силовом поле, то есть, когда потенциальная энергия частицы U ≠ 0. В этом случае выражение

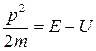определяет энергию движения частицы (аналог кинетической энергии в классической механике). После подстановки значений Е и p получаем:

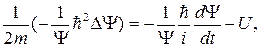
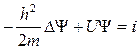ħ .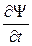

Полученное выражение совпадает с уравнением Шрёдингера (21.7) для частицы, движущейся в силовом поле.