Вопрос 2. Уравнение Шрёдингера.

Построение строго математического аппарата квантовой механики невозможно без уравнения, которое позволило бы по заданным внешним силовым полям и начальным условиям описывать движение частицы в пространстве и во времени.

Поскольку состояние квантовой частицы задается волновой функцией 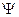(x,y,z,t), точнее величиной | 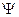(x,y,z,t)|², определяющей плотность вероятности нахождения частицы в момент времени t в точке с координатами (x,y,z), то искомое уравнение должно быть уравнением относительно функции 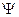. Это уравнение должно обладать некоторыми чертами, присущими волновому уравнению для упругих волн, поскольку оно призвано учитывать волновые свойства микрочастиц.

Уравнение, удовлетворяющее перечисленным требованиям, было найдено в 1926 г. австрийским физиком Шрёдингером и называется уравнением Шрёдингера:

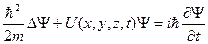− , (21.7)

где i = 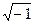- мнимая единица; m -- масса частицы; ∆ − оператор Лапласа, который в декартовой системе имеет вид 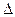= 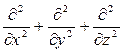, U(x,y,z,t) – потенциальная энергия частицы во внешнем силовом поле в точке с координатами (x,y,z) (Нобелевская премия по физике присуждена Шрёдингеру в 1933г.), тогда

.

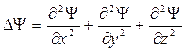Таким образом, уравнение (21.7) представляет собой линейное однородное дифференциальное уравнение в частных производных. Здесь представлена искомая переменная функция 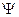(x,y,z,t), частная производная этой функции по времени и частные производные второго порядка этой функции по координатам.

Уравнение (21.7) было именно найдено, его невозможно вывести из прежних теорий. Справедливость этого уравнения установлена тем, что все вытекающие из него следствия подтверждены экспериментом. Если функция U не зависит явно от времени, т.е. U ≠ f(t), то она имеет смысл потенциальной энергии микрочастицы. Вид 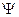- функции для конкретной микрочастицы определяется именно потенциальной энергией микрочастицы U. В этом случае уравнение Шрёдингера несколько упрощается, так как его решение можно искать методом разделения переменных, т.е. 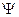- функцию можно представить в виде произведения двух сомножителей, один из которых зависит только от координат, а другой − только от времени:

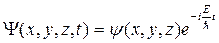, (21.8)

где Е - полная энергия частицы. Подставим полученное выражение для

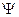-функции в уравнение (21.7):

− .

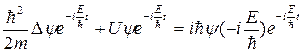После деления уравнения на множитель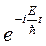 имеем:

.

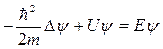Полученноесоотношение называется уравнением Шрёдингера для стационарных состояний. Поле стационарно, когда его характеристики не зависят от времени, например, для состояний с фиксированными значениями энергии. Это уравнение часто записывают в виде:

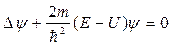. (21.9)

В стационарных состояниях ни одна из квантовомеханических вероятностей не изменяется с течением времени. Средние значения всех физических величин также не зависят от времени. В частичности, постоянным во времени оказывается среднее значение координаты < x >. Стационарность состояние не исключает зависимость волновой функции от времени, а только ограничивает ее множителем 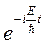. Состояние (21.9) стационарно, так как равен единице модуль множителя 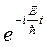,то есть,

.

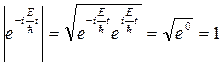Поэтому плотность распределения координат частиц

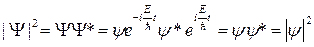
от времени не зависит. В стационарном состоянии плотность вероятности выражается только через функцию 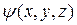. Поэтому функцию 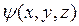также называется волновой функцией, хотя, строго говоря, она является только координатной частью всей волновой функции 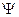(x,y,z,t) стационарного состояния.