Вопрос 3. Постулаты Бора и объяснение происхождения линейчатых спектров. Закономерности в атомных спектрах.

Опытные данные об атоме водорода. Естественно начинать изучение структуры атомов с самого простого атома – атома водорода. Ко времени создания теории Бора об атоме водорода имелись следующие экспериментальные сведения. Атом водорода состоит из ядра (протона), несущего положительный заряд, равный по величине заряду электрона, и одного электрона, который согласно планетарной модели Резерфорда, движется вокруг ядра по круговой или эллиптической орбите. Размеры атома водорода определяются диаметром орбиты электрона и составляют несколько больше 10^{-10 м}.

Наиболее важные для создания теории атомов сведения были получены из спектра излучения водорода. Спектр водорода оказался наиболее простым по сравнению со спектрами других элементов. В нем были обнаружены удивительно простые и в то же время выполняющиеся с очень большой точностью закономерности в расположении спектральных линий, так называемые спектральные серии (спектральные серии были найдены также и в спектрах других элементов, но формулы для их описания оказались более сложными, а совпадение этих формул с опытом значительно менее точным). Оказалось, что частоты всех линий, которые наблюдаются в спектре излучения водорода, определяются формулой:

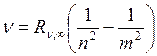. (19.2)

Это обобщенная формула Бальмера. Здесь ν – частота световой волны, 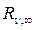– постоянная Ридберга ( 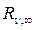=3,293 · 10¹⁵ c^-1, n=1,2,3 …, m=2, 3, 4 …) .

Ядерная модель атома в сочетании с классической механикой и электродинамикой оказалась неспособной объяснить ни устойчивость атома, ни характер атомного спектра. Выход из создавшегося тупика был найден в 1913 г. датским физиком Нильсом Бором, правда, ценой введения предположений, противоречащих классическим представлениям. Допущения, сделанные Бором, содержатся в двух высказанных им постулатах.

1.Первый постулат Бора (постулат стационарных состояний) гласит: из бесконечного множества электронных орбит, возможных с точки зрения классической механики, осуществляются в действительности только некоторые дискретные орбиты, удовлетворяющие определенным квантовым условиям. Электрон, находящийся на одной из этих орбит, несмотря на то, что он движется с ускорением, не излучает электромагнитных волн (света).

Согласно первому постулату атом характеризуется системой энергетических уровней, каждый из которых соответствует определенному стационарному состоянию. Стационарным состояниям соответствуют стационарные орбиты, по которым электрон может вращаться вокруг ядра неопределенно долго, не излучая энергию. Энергия атома может измениться лишь при скачкообразном переходе электрона из одного энергетического состояния в другое.

2. Второй постулат Бора (правило частот)формулируется следующим образом: излучение испускается или поглощается в виде светового кванта энергии 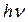при переходе электрона из одного стационарного (устойчивого) состояния в другое (рис. 19.4). Величина светового кванта равна разности энергий тех стационарных состояний, между которыми совершается квантовый переход электрона:

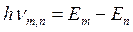. (19.3)

Отсюда следует, что изменение энергии атома, связанное с излучением при поглощении фотона, пропорционально частоте ν:

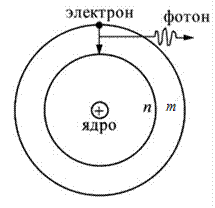
Рис. 19.4

поглощении фотона, пропорционально частоте ν:

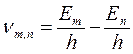, (19.4)

т.е. частота излучаемого света может быть представлена в виде разности двух величин, характеризующих энергию излучающей системы.

Второй постулат Бора также противоречит электродинамике Максвелла. По Бору частота излучения определяется только изменением энергии атома и никак не зависит от характера движения электрона. А согласно Максвеллу (т.е. с точки зрения классической электродинамики) частота излучения зависит от характера движения электрона.

Важную роль в развитии планетарной модели сыграли эмпирические закономерности, полученные для линейчатого спектра атома водорода.

В 1858 г. швейцарский физик И. Бальмер установил, что частоты девяти линий в видимой области спектра водорода удовлетворяют соотношению

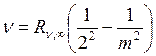, m=3, 4, 5, …, 11. (19.5)

Открытие водородной серии Бальмера (19.5) послужило толчком для обнаружения других серий в спектре атома водорода в начале 20 века.

Из формулы (19.5) видно, что по мере увеличения m частота 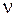линий спектра возрастает, при этом интервалы между соседними частотами уменьшаются, так что при 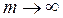частота 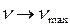. Максимальное значение частоты в серии Бальмера, полученное при 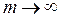, называется границейсерии Бальмера, за пределами которой находится непрерывный спектр.

В ультрафиолетовой области спектра водорода находится серия Лаймана:

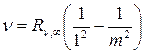, m = 2,3,4… (19.6)

В инфракрасной области расположены еще четыре серии:

Серия Пашена, 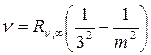, m = 4,5,6…

Серия Брэкета 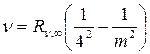, m = 5,6,7… (19.7)

Серия Пфунда 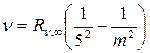, m = 6,7,8…

Серия Хэмфри 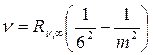, m = 7,8,9…

Как уже отмечалось, частоты всех линий спектра атома водорода представляются одной формулой (19.2).

Частота линии в каждой серии стремится к предельному максимальному значению 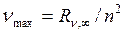, которое называется границейсерии. Спектральные серии Лаймана и Бальмера обособлены, остальные серии частично перекрываются. Например, границы (длины волн) первых трех серий (Лаймана, Бальмера, Пашена) соответственно равны

0,0912 мкм; 0,3648 мкм; 0, 8208 мкм (λ_min = c/ν_max ).

Бором было введено правило квантования орбит, которое гласит: в стационарном состоянии атома электрон, двигаясь по круговой орбите

радиуса r, должен иметь дискретные, т.е. квантованные, значения момента импульса, удовлетворяющие условию:

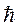
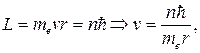n = 1, 2, 3…, (19.8)

где n – главное квантовое число, 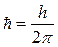– также постоянная Планка.

Дискретность радиусов орбит и энергии стационарных состояний.Рассмотрим электрон (рис. 19.5), движущийся со скоростью V в поле атомного ядра с зарядом Ze. Квантовая система, состоящая из ядра и только одного электрона, называется водородноподобным атомом. Таким образом, термин «водородноподобный атом» применим, помимо атома водорода, у которого Z = 1, к однократно ионизированному атому гелия Hе⁺, к двукратно ионизированному атому лития Li⁺² и т. д.

На электрон, движущийся по круговой стационарной орбите, действует электрическая, т.е. кулоновская сила притяжения со стороны ядра,

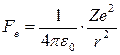, (19.9)

Рис. 19.5

которая компенсируется центробежной силой:

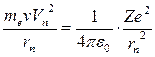. (19.10)

Подставив в формулу (19.10) выражение для скорости из (19.8) и решив полученное уравнение относительно r_n, получим набор дискретных значений радиусов орбит электрона в водородоподобных атомах:

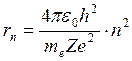, (19.11)

где n = 1,2,3… .

С помощью формулы (19.11) определяют радиусы разрешенных стационарных орбит в боровской полуквантовой модели атома. Число n = 1 соответствует ближайшей к ядру орбите, поэтому для атома водорода (Z=1) радиус первой орбиты

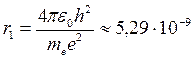м, (19.12)

а соответствующая этой орбите скорость электрона

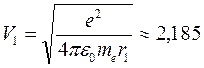км/c.

Наименьший радиус орбиты называется первым боровским радиусом ( 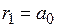). Из выражения (19.11) видно, что радиусы более далеких от ядра орбит для водородоподобных атомов увеличиваются пропорционально квадрату числа n (рис. 19.6)

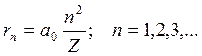(19.13)

Рис. 19.6

Теперь рассчитаем для каждой из разрешенных орбит полную энергию электрона, которая состоит из его кинетической и потенциальной энергий:

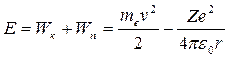. (19.14)

Напомним, что потенциальная энергия электрона в поле положительно заряженного ядра является величиной отрицательной. Подставляя в выражение (19.14) значение скорости V из (19.8), а затем, используя формулу (19.13) для r, получаем (с учетом того, что ):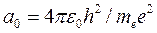

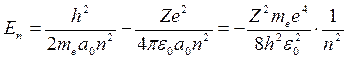, n = 1, 2, 3 … (19.15)

Отрицательный знак в выражении (19.15) для энергии атома обусловлен тем, что за нулевое значение потенциальной энергии электрона принято считать то значение, которое соответствует удалению электрона на бесконечность от ядра.

Орбита с самым малым радиусом соответствует наименьшему значению энергии и называется К - орбитой, за ней следует L- орбита, М – орбита и т.д. При движении электронов по этим орбитам атом находится в устойчивом состоянии. Схема энергетических уровней для спектральных серий атома водорода, определяемых уравнением (19.15), изображена на рис. 19.7. Горизонтальные линии соответствуют энергиям стационарных состояний.

Расстояния между энергетическими уровнями пропорциональны квантам энергий, испускаемых атомом при соответствующих переходах электрона (изображены стрелками). При поглощении атомом квантов энергии направления стрелок следует изменить на противоположные.

Из выражения (19.14) видно, что в планетарной модели Бора энергетические состояния атома водорода характеризуются бесконечной последовательностью энергетических уровней E_n. Значения E_n обратно пропорциональны квадрату числа n, которое называется главным квантовым числом. Энергетическое состояние атома с n=1 называется основным или нормальным, т.е. невозбужденным состоянием, которое соответствует минимальному значению энергии. Если n > 1, состояние атома является возбужденным ( ).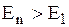

Энергия E₁ основного состояния атома водорода из (19.15) равна

– 13,53 эВ.

Энергия ионизацииатома водорода,т.е. E_i = │E₁ - E_∞│= 13,53 эВ, равна работе, совершаемой при перемещении электрона из основного состояния (n = 1) в бесконечность без сообщения ему кинетической энергии.

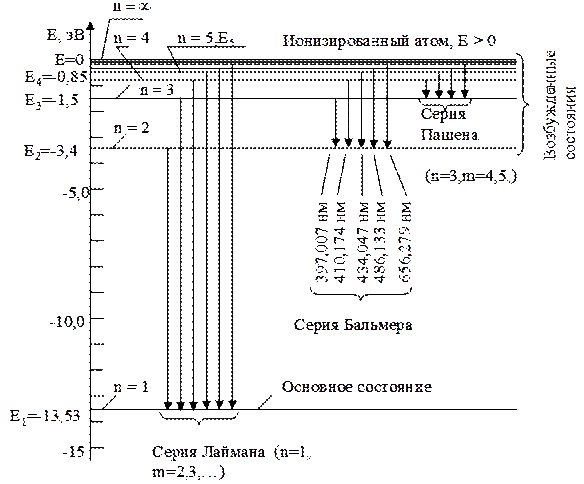
Рис.19.7

Спектральные закономерности.В соответствии со вторым постулатом Бора при переходе электрона атома водорода из возбужденного состояния в состояние, соответствующее уровню n( n<m ) атом водорода испускает квант электромагнитного излучения с частотой

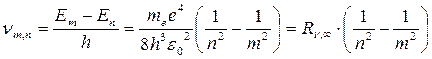, (19.16)

откуда 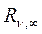= =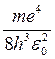3,29·10¹⁵ с^-1. (19.17)

От частоты 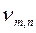можно перейти к длине волны :

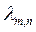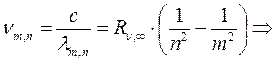
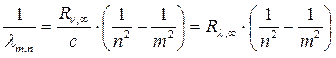, (19.18)

где величина

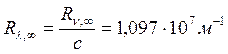, (19.19)

которую также называют постоянной Ридберга. Для перехода электрона в атоме водорода с n-го энергетического уровня (n-ой орбиты) на m-ый энергетический уровень (m-ую орбиту) при n<m атому необходимо сообщить энергию, равную разности энергий атома в конечном и начальном состояниях.

Таким образом, модель атома Н. Бора объясняет дискретный (линейчатый) характер спектра излучения атома водорода.

Опыт Франка и Герца.Существование дискретных энергетических уровней атомов подтверждается опытом Д. Франка и Г. Герца, которые за экспериментальные исследования дискретности энергетических уровней в атомах получили Нобелевскую премию (1925 г.).

В опытах использовалась трубка (рис. 19.8), заполненная парами ртути при давлении р ≈ 1 мм рт. ст. и три электрода: катод К, сетка С и анод А и измерять вольтметром V. Электроны ускорялись разностью потенциалов U между катодом и сеткой. Эту разность потенциалов можно было изменять с помощью потенциометра П. Между сеткой и анодом создавалось тормозящее поле 0,5 В (метод задерживающих потенциалов). Определялась зависимость тока через гальванометр Г от разности потенциалов U между катодом и сеткой.

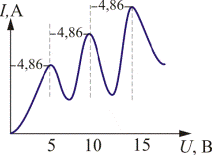
Рис. 19.8 Рис. 19.9

В эксперименте была получена зависимость, изображенная на рис. 19.9. Здесь U = 4,86 В – соответствует первому потенциалу возбуждения атома.

Согласно боровской теории, каждый из атомов ртути может получить лишь вполне определенную энергию, переходя в одно из возбужденных состояний. Поэтому если в атомах действительно существуют стационарные состояния, то электроны, сталкиваясь с атомами ртути, должны терять энергию дискретно, определенными порциями, равными разности энергии соответствующих стационарных состояний атома.

Из опыта следует, что при увеличении ускоряющего потенциала вплоть до 4,86 В анодный ток возрастает монотонно, его значение проходит через максимум при 4,86 В, затем резко уменьшается и возрастает вновь. Дальнейшие максимумы наблюдаются при значениях, кратных значению 4,86 В ускоряющего потенциала, т.е. 2·4,86 В и 3·4,86 В. Ближайшим к основному, невозбужденному состоянию атома ртути является возбужденное состояние, отстоящее по шкале энергий на 4,86 В. Пока разность потенциалов между катодом и сеткой меньше 4,86 В, электроны, встречая на своем пути атомы ртути, испытывают с ними только упругие соударения. При eφ = 4,86 эВ энергия электрона становится достаточной, чтобы вызвать неупругий удар, при котором электрон отдает атому ртути всю кинетическую энергию, возбуждая переход одного из электронов атома из нормального состояния в возбужденное. Электроны, потерявшие свою кинетическую энергию, уже не смогут преодолеть тормозящий потенциал и достигнуть анода. Этим и объясняется резкое падение анодного тока при eφ = 4,86 эВ.

При значениях энергии, кратных 4,86 эВ, электроны могут испытывать с атомами ртути 2, 3, … неупругих соударения. При этом они полностью теряют свою энергию и не достигают анода, т.е. наблюдается резкое падение анодного тока. Таким образом, опыт показал, что электроны передают своюэнергию атомам ртути порциями, причем 4,86 эВ – наименьшая возможная порция, которая может быть поглощена атомом ртути в основном энергетическом состоянии. Следовательно, идея Бора о существовании в атомах стационарных состояний блестяще выдержала проверку экспериментом.

Атомы ртути, получившие при соударении с электронами энергию ΔE , переходят в возбужденное состояние и должны вернуться в основное, излучая при этом, согласно второму постулату Бора, квант света с частотой ν = ΔE / h. По известному значению ΔE = 4,86 В можно вычислить длину волны светового кванта: λ = hс / ΔE ≈ 255 нм. Таким образом, если теория верна, то атомы ртути, бомбардируемые электронами с энергией 4,86 эВ, должны являться источником ультрафиолетового излучения с λ ≈ 255 нм, что действительно обнаружилось в опытах.

Таким образом, опыты Франка и Герца экспериментально подтвердили не только первый, но и второй постулат Бора и внесли большой вклад в развитие атомной физики.

Для водородоподобных ионов обобщенная сериальная формула Бальмера-Ридберга имеет вид:

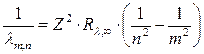. (19.20)

Используя постоянную Ридберга, получим выражение для энергии атома водорода:

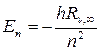, (19.21)

или 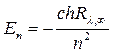. (19.22)

При n = 1 эта энергия равна работе ионизации атома водорода, т.е.

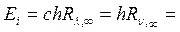׀e׀ U_i, (19.23)

где 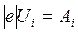, U_i – потенциал ионизации, т.е. та наименьшая разность потенциалов, которую должен пройти электрон в электрическом поле, чтобы при столкновении с данным невозбужденным атомом ионизировать его. Работа по удалению электрона из атома равна работе сил электрического поля, ускоряющего электрон. Различают также потенциалы возбуждения атома. Например, первый потенциал возбуждения φ₁ – это ускоряющее напряжение, соответствующее переходу невозбужденного атома в первое возбужденное состояние. Учитывая квантовый характер поглощения энергии атомом, можно утверждать, что работа ионизации (или работа по возбуждению атома) равна энергии кванта hν, поглощенной атомом водорода при переходе электрона с первой боровской орбиты в бесконечность (или, например, на вторую орбиту).

Постоянная Ридберга (19.16) или (19.18) вычислена в предположении, что в атоме водорода электрон вращается вокруг «неподвижного» ядра, что возможно, строго говоря, при условии, когда масса ядра бесконечно велика в сравнении с массой электрона, поэтому эту постоянную часто снабжают индексом .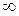

На самом же деле ядро и электрон вращаются вокруг их общего центра масс, что приводит к несколько иному значению для этой постоянной:

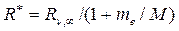, (19.24)

где M – масса атомного ядра. Это обстоятельство учитывается на практике и при решении некоторых задач, где речь идет о сравнении спектров различных атомов. Например, благодаря чрезвычайной точности спектроскопических методов, появляется возможность экспериментально обнаружить различие в спектрах излучения изотопов водорода - атомов, отличающихся массами ядер. Практически, именно так, спектроскопическими методами был открыт изотоп тяжелого водорода - дейтерий D, для которого M_D= 2M_H.

Теория Бора стала важным шагом в развитии физики атома. Она позволила объяснить механизм возникновения спектров и рассчитать частоты спектральных линий атома водорода и водородоподобных атомов (Нобелевская премия, 1922 год). Однако возникли принципиальные трудности при попытке использовать ее для объяснения спектральных закономерностей сложных атомов, содержащих более одного электрона, и молекул, а также для объяснения механизма образования молекул из атомов, т.е. при создании физической теории химических реакций. Кроме того, теория Бора является непоследовательной, поскольку введенное в нее Бором правило квантования момента импульса в принципе несовместимо с используемым классическим описанием поведения электрона. Сущность этого несоответствия выявилась лишь в 1924 году благодаря гипотезе де Бройля, которая позволила корпускулярно-волновой дуализм света распространить на микрочастицы.

Модель Бора не позволяет дать физическую интерпретацию правилу квантования. Это было сделано десятилетием позже де Бройлем на основе представлений о волновых свойствах частиц. Де Бройль предположил, что каждая орбита в атоме водорода соответствует волне, распространяющейся по окружности около ядра атома. Стационарная орбита возникает в том случае, когда волна непрерывно повторяет себя после каждого оборота вокруг ядра. Другими словами, стационарная орбита соответствует круговой стоячей волне де Бройля на длине орбиты (рис 19.10). Здесь показаны стоячие волны де Бройля, укладывающиеся вдоль круговой орбиты. Орбита показана тонкой линией, n – число полных волн, укладывающихся вдоль нее.

Рис 19.10

Рис. 19.9

Это явление очень похоже на стационарную картину стоячих волн в струне с закрепленными концами. В стационарном квантовом состоянии атома водорода на длине орбиты должно укладываться по идее де Бройля целое число длин волн λ_n, т.е. nλ_n=2πr_n. В результате, боровское правило квантования оказалось связанным с волновыми свойствами электронов.