Формулы Эйлера и Ясинского
Для расчетов стержней на устойчивость необходимо знать способы определения критической силы Fкр.
Первые исследования устойчивости сжатых стержней были проведены академиком Петербургской Академии наук Леонардом Эйлером (1707—1783). Академик С. И. Вавилов писал: «Вместе с Петром I и Ломоносовым Эйлер стал добрым гением нашей Академии, определившим ее славу, ее крепость, ее продуктивность». В дальнейшем большая работа в области теоретического и экспериментального исследования вопросов устойчивости была проведена русским ученым, профессором Петербургского института инженеров путей сообщения Ф. С. Ясинским (1856—1899)у опубликовавшим в 1893 г. большую работу «Опыт развития продольного изгиба».
Л. Эйлером была получена формула для определения величины критической силы Fкр.
Приведем ф о р м у л у Эйлера без вывода:
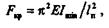
где Е — модуль упругости первого рода; Imin — наименьший из осевых
моментов инерции сечения, поскольку искривление стержня происходит в плоскости наименьшей жесткости, в чем нетрудно убедиться, сжимая продольной силой слесарную линейку; lп — приведенная длина стержня;
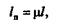
где l— длина стержня; 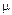 — коэффициент приведения длины, зависящий от способа закрепления концов стержня.
— коэффициент приведения длины, зависящий от способа закрепления концов стержня.
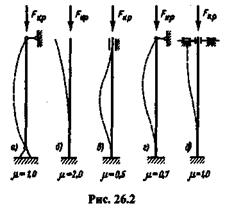
На рис. 26.2 показаны наиболее часто встречающиеся способы закрепления концов стержня и приведены значения 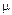 : 1) оба конца стержня закреплены шарнирно и могут сближаться (а); 2) нижний конец жестко защемлен, верхний свободен (б); 3) оба конца жестко защемлены, но могут сближаться (в); 4) нижний конец закреплен жестко, верхний — шарнирно, концы могут сближаться (г); 5) нижний конец закреплен жестко,
: 1) оба конца стержня закреплены шарнирно и могут сближаться (а); 2) нижний конец жестко защемлен, верхний свободен (б); 3) оба конца жестко защемлены, но могут сближаться (в); 4) нижний конец закреплен жестко, верхний — шарнирно, концы могут сближаться (г); 5) нижний конец закреплен жестко,
|
верхний имеет «плавающую заделку» (д).Заметим, что чем меньше 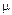 , тем больше критическая сила, а следовательно, и допускаемая сжимающая нагрузка. Например, сжимающая нагрузка стержня, жестко защемленного обоими концами (
, тем больше критическая сила, а следовательно, и допускаемая сжимающая нагрузка. Например, сжимающая нагрузка стержня, жестко защемленного обоими концами ( 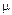 = 0,5), может быть в 16 раз больше нагрузки стержня, защемленного одним концом (
= 0,5), может быть в 16 раз больше нагрузки стержня, защемленного одним концом ( 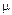 = 2).
= 2).
Вывод формулы Эйлера основан на законе Гука, который справедлив только до пре-
| Определим наименьший радиус инерции imin поперечного сечения стержня: |
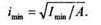
|
Перепишем формулу для 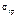 так: так:
|
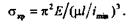
|
дела пропорциональности. Поэтому формулой Эйлера можно пользоваться не всегда. Для определения пределов применимости формулы Эйлера определим критическое напряжение 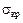 , т.е. напряжение, которое возникает в поперечном сечении площадью А стержня при достижении
, т.е. напряжение, которое возникает в поперечном сечении площадью А стержня при достижении
 критической силы:
критической силы:
Введем понятие гибкости стержня 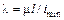 . Это безразмерная величина, характеризующая размеры стержня и способ закрепления его концов. Окончательно получаем:
. Это безразмерная величина, характеризующая размеры стержня и способ закрепления его концов. Окончательно получаем:
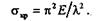
Формулу Эйлера можно применять только при выполнении условия
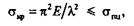
где 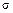 пц — предел пропорциональности материала стержня. Следовательно, должно быть
пц — предел пропорциональности материала стержня. Следовательно, должно быть
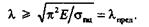
Величину, стоящую в правой части неравенства, называют предельной гибкостью. Предельная гибкость зависит только от физико-механических свойств материала стержня.
Условие применимости формулы Эйлера можно записать так:
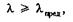
т. е. формула Эйлера применима лишь в тех случаях, когда гибкость стержня больше или равна предельной гибкости.
Вычислим значение 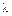 пред для низкоуглеродистой стали Ст3, для которой
пред для низкоуглеродистой стали Ст3, для которой 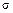 пц = 200 МПа, а Е = 2
пц = 200 МПа, а Е = 2  105 МПа:
105 МПа:
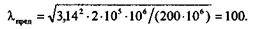
Для стержней из низкоуглеродистой стали формула Эйлера применима, если их гибкость 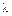
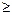 100.
100.
Аналогично можно вычислить значения предельной гибкости для других материалов. В частности, для чугуна 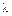 пред = 80; для дерева (сосна)
пред = 80; для дерева (сосна) 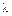 пред =110.
пред =110.
|
В тех случаях, когда гибкость стержней меньше предельной, формула Эйлера становится неприменимой и при расчетах пользуются эмпирической формулой Ясинского
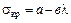
где а и b — коэффициенты, зависящие от материала и определяемые по таблицам справочников. В частности, для СтЗ при гибкостях 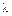 = 40...100 можно принимать
= 40...100 можно принимать
а =310 МПа, b= 1,14 МПа. При гибкостях 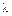 < 40 стержни можно рассчитывать на сжатие, т.е. по формуле
< 40 стержни можно рассчитывать на сжатие, т.е. по формуле
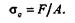
Итак, при малых значениях 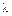 (
( 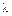 < 40) стержни из низкоуглеродистой стали рассчитывают на простое сжатие; при средних значениях (40
< 40) стержни из низкоуглеродистой стали рассчитывают на простое сжатие; при средних значениях (40 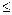
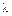 < 100) расчет ведут по формуле Ясинского, а при больших (
< 100) расчет ведут по формуле Ясинского, а при больших ( 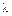
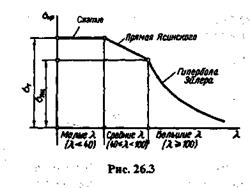
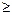 100) — по формуле Эйлера. График зависимости критического напряжения от гибкости для стержней из низкоуглеродистой стали изображен на рис. 26.3.
100) — по формуле Эйлера. График зависимости критического напряжения от гибкости для стержней из низкоуглеродистой стали изображен на рис. 26.3.
Дата добавления: 2021-09-07; просмотров: 1050;











